
【题目】下列所给条件中,不能判断两个直角三角形全等的是( )
A. 一个锐角和这个锐角的对边对应相等B. 一个锐角与斜边对应相等
C. 两锐角对应相等D. 一锐角和一边对应相等
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用一条24cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王星期天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接八位乘客的行车里程(单位:![]() ):-3,+6,-1,-2,+4,-2,+5,-4.
):-3,+6,-1,-2,+4,-2,+5,-4.
问:(1)将最后一位乘客送到目的地时,小王在什么位置?
(2)若汽车耗油量为![]() ,这天上午小王接送乘客,出租车共耗油多少升?
,这天上午小王接送乘客,出租车共耗油多少升?
(3)若出租车的起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.5元,则小王这天上午共得车费多少元?
),超过部分每千米1.5元,则小王这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
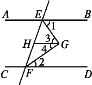
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,顶点为
两点,顶点为![]() .
.
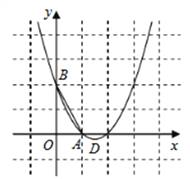
(1)求抛物线的解析式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,点
后,点![]() 落在点
落在点![]() 的位置,将抛物线沿
的位置,将抛物线沿![]() 轴平移后经过点
轴平移后经过点![]() ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,8为半径的圆与
为圆心,8为半径的圆与![]() 轴交于
轴交于![]() ,
,![]() 两点,过
两点,过![]() 作直线
作直线![]() 与
与![]() 轴负方向相交成
轴负方向相交成![]() 的角,且交
的角,且交![]() 轴于
轴于![]() 点,以点
点,以点![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于点
轴相切于点![]() .
.
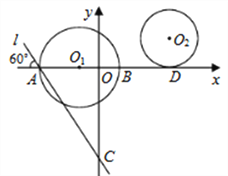
(1)求直线![]() 的解析式;
的解析式;
(2)将![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 轴向左平移,当
轴向左平移,当![]() 第一次与
第一次与![]() 外切时,求
外切时,求![]() 平移的时间.
平移的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(0,4),B(﹣2,2),C(3,0).
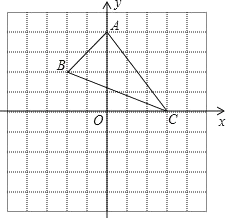
(1)作△ABC关于x轴对称的△A1B1C1;
(2)△A1B1C1的面积= .A1C1边上的高= ;
(3)在x轴上有一点P,使PA+PB最小,此时PA+PB的最小值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直径是![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
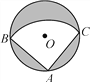
(1)AB的长为多少米?
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面半径为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com