
ЁОЬтФПЁПШчЭМ1ЃЌНЋБпГЄЮЊ1ЕФе§ЗНаЮABCDбЙБтЮЊБпГЄЮЊ1ЕФСтаЮABCDЃЎдкСтаЮABCDжаЃЌЁЯAЕФДѓаЁЮЊІСЃЌУцЛ§МЧЮЊSЃЎ
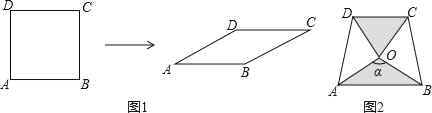
ЃЈ1ЃЉЧыВЙШЋБэЃК
ІС | 30Ёу | 45Ёу | 60Ёу | 90Ёу | 120Ёу | 135Ёу | 150Ёу |
S |
| 1 |
|
ЃЈ2ЃЉЬюПеЃК
гЩЃЈ1ЃЉПЩвдЗЂЯжЕЅЮЛе§ЗНаЮдкбЙБтЕФЙ§ГЬжаЃЌСтаЮЕФУцЛ§ЫцзХЁЯAДѓаЁЕФБфЛЏЖјБфЛЏЃЌВЛЗСАбЕЅЮЛСтаЮЕФУцЛ§SМЧЮЊSЃЈІСЃЉЃЎР§ШчЃКЕБІСЃН30ЁуЪБЃЌSЃНSЃЈ30ЁуЃЉЃН![]() ЃЛЕБІСЃН135ЁуЪБЃЌSЃНSЃЈ135ЁуЃЉЃН
ЃЛЕБІСЃН135ЁуЪБЃЌSЃНSЃЈ135ЁуЃЉЃН![]() ЃЎгЩЩЯБэПЩвдЕУЕНSЃЈ60ЁуЃЉЃНSЃЈЁЁ ЁЁЁуЃЉЃЛSЃЈ150ЁуЃЉЃНSЃЈЁЁ ЁЁЁуЃЉЃЌЁЃЌгЩДЫПЩвдЙщФЩГіSЃЈ180ЁуЉІСЃЉЃНЃЈЁЁ ЁЁЁуЃЉЃЎ
ЃЎгЩЩЯБэПЩвдЕУЕНSЃЈ60ЁуЃЉЃНSЃЈЁЁ ЁЁЁуЃЉЃЛSЃЈ150ЁуЃЉЃНSЃЈЁЁ ЁЁЁуЃЉЃЌЁЃЌгЩДЫПЩвдЙщФЩГіSЃЈ180ЁуЉІСЃЉЃНЃЈЁЁ ЁЁЁуЃЉЃЎ
ЃЈ3ЃЉСНПщЯрЭЌЕФЕШбќжБНЧШ§НЧАхАДЭМ2ЕФЗНЪНЗХжУЃЌADЃН![]() ЃЌЁЯAOBЃНІСЃЌЪдЬНОПЭМжаСНИіДјвѕгАЕФШ§НЧаЮУцЛ§ЪЧЗёЯрЕШЃЌВЂЫЕУїРэгЩЃЈзЂЃКПЩвдРћгУЃЈ2ЃЉжаЕФНсТлЃЉЃЎ
ЃЌЁЯAOBЃНІСЃЌЪдЬНОПЭМжаСНИіДјвѕгАЕФШ§НЧаЮУцЛ§ЪЧЗёЯрЕШЃЌВЂЫЕУїРэгЩЃЈзЂЃКПЩвдРћгУЃЈ2ЃЉжаЕФНсТлЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ120ЃЛ30ЃЛІСЃЈ3ЃЉСНИіДјвѕгАЕФШ§НЧаЮУцЛ§ЯрЕШ
ЃЈ2ЃЉ120ЃЛ30ЃЛІСЃЈ3ЃЉСНИіДјвѕгАЕФШ§НЧаЮУцЛ§ЯрЕШ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§DзїDEЁЭABгкЕуEЃЌЕБІСЃН45ЁуЪБЃЌПЩЧѓЕУDEЃЌДгЖјПЩЧѓЕУСтаЮЕФУцЛ§SЃЌЭЌРэПЩЧѓЕБІСЃН60ЁуЪБSЕФжЕЃЌЕБІСЃН120ЁуЪБЃЌЙ§DзїDFЁЭABНЛBAЕФбгГЄЯпгкЕуFЃЌдђПЩЧѓЕУDFЃЌПЩЧѓЕУSЕФжЕЃЌЭЌРэЕБІСЃН135ЁуЪБSЕФжЕЃЛ
ЃЈ2ЃЉИљОнБэжаЫљМЦЫуГіЕФSЕФжЕЃЌПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉНЋЁїABOбиABЗелЕУЕНСтаЮAEBOЃЌНЋЁїCDOбиCDЗелЕУЕНСтаЮOCFDЃЎРћгУЃЈ2ЃЉжаЕФНсТлЃЌПЩЧѓЕУЁїAOBКЭЁїCODЕФУцЛ§ЃЌДгЖјПЩЧѓЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЕБІСЃН45ЁуЪБЃЌШчЭМ1ЃЌЙ§DзїDEЁЭABгкЕуEЃЌ

дђDEЃН![]() ADЃН
ADЃН![]() ЃЌ
ЃЌ
ЁрSЃНABDEЃН![]() ЃЌ
ЃЌ
ЭЌРэЕБІСЃН60ЁуЪБSЃН![]() ЃЌ
ЃЌ
ЕБІСЃН120ЁуЪБЃЌШчЭМ2ЃЌЙ§DзїDFЁЭABЃЌНЛBAЕФбгГЄЯпгкЕуFЃЌ
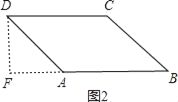
дђЁЯDAEЃН60ЁуЃЌ
ЁрDFЃН![]() ADЃН
ADЃН![]() ЃЌ
ЃЌ
ЁрSЃНABDFЃН![]() ЃЌ
ЃЌ
ЭЌРэЕБІСЃН150ЁуЪБЃЌПЩЧѓЕУSЃН![]() ЃЌ
ЃЌ
ЙЪБэжавРДЮЬюаДЃК![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊSЃЈ60ЁуЃЉЃНSЃЈ120ЁуЃЉЃЌ
SЃЈ150ЁуЃЉЃНSЃЈ30ЁуЃЉЃЌ
ЁрSЃЈ180ЁуЉІСЃЉЃНSЃЈІСЃЉ
ЙЪД№АИЮЊЃК120ЃЛ30ЃЛІСЃЛ
ЃЈ3ЃЉСНИіДјвѕгАЕФШ§НЧаЮУцЛ§ЯрЕШЃЎ
жЄУїЃКШчЭМ3НЋЁїABOбиABЗелЕУЕНСтаЮAMBOЃЌНЋЁїCDOбиCDЗелЕУЕНСтаЮOCNDЃЎ
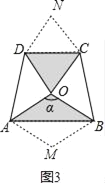
ЁпЁЯAODЃНЁЯCOBЃН90ЁуЃЌ
ЁрЁЯCOD+ЁЯAOBЃН180ЁуЃЌ
ЁрSЁїAOBЃН![]() SСтаЮAMBOЃН
SСтаЮAMBOЃН![]() SЃЈІСЃЉ
SЃЈІСЃЉ
SЁїCDOЃН![]() SСтаЮOCNDЃН
SСтаЮOCNDЃН![]() SЃЈ180ЁуЉІСЃЉ
SЃЈ180ЁуЉІСЃЉ
гЩЃЈ2ЃЉжаНсТлSЃЈІСЃЉЃНSЃЈ180ЁуЉІСЃЉ
ЁрSЁїAOBЃНSЁїCDOЃЎ


 ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ
ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ бЇЯАЪЕМљдАЕиЯЕСаД№АИ
бЇЯАЪЕМљдАЕиЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
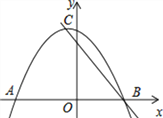
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкЕуAЃЈЉ2ЃЌ0ЃЉЁЂBЃЈx1ЃЌ0ЃЉЃЌЧв1ЃМx1ЃМ2ЃЌгыyжсе§АыжсЕФНЛЕудкЃЈ0ЃЌ2ЃЉЕФЩЯЗНЃЌЖЅЕуЮЊCЃЎжБЯпy=kx+mЃЈkЁй0ЃЉОЙ§ЕуCЁЂBЃЎдђЯТСаНсТлЃКЂйbЃОaЃЛЂк2aЉbЃОЉ1ЃЛЂл2a+cЃМ0ЃЛЂмkЃОa+bЃЛЂнkЃМЉ1. Цфжае§ШЗЕФНсТлга_________ЃЎЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖзщжЏЪ§бЇМЮФъЛЊЛюЖЏЃЌЙВЦРГіШ§ИіНБЯюЃЌФъМЖДІЙКТђСЫвЛаЉНБЦЗНјааБэеУЃЌЯрЙиЭГМЦНсЙћШчЯТБэЃЈВЛЭъећЃЉЫљЪОЃК
вЛЕШНБ | ЖўЕШНБ | Ш§ЕШНБ | КЯМЦ | |
ЛёНБШЫЪ§(ЕЅЮЛЃКШЫ) | 40 | |||
НБЦЗЕЅМл(ЕЅЮЛЃКдЊ) | 12 | 9 | 6 | |
НБЦЗН№Жю(ЕЅЮЛЃКдЊ) | 300 |
вбжЊЖўЕШНБЕФЛёНБШЫЪ§БШвЛЕШНБЕФЛёНБШЫЪ§Жр5ШЫЃЎФуФмИљОнЫљИјЬѕМўЃЌЗжБ№ЧѓГіШ§жжНБЯюЕФЛёНБШЫЪ§Т№ЃПЧыИљОнФуЫљЩшЕФЮДжЊЪ§ЃЌЯШЬюБэ(ДњЪ§ЪНВЛБиЛЏМђ)ЃЌдйСаЗНГЬНтД№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧАДеевЛЖЈЙцТЩЛГіЕФвЛСаЁАЪїаЭЁБЭМЃК

ОЙлВьПЩвдЗЂЯжЃКЭМЃЈ2ЃЉБШЭМЃЈ1ЃЉЖрГі2ИіЁАЪїжІЁБЃЌЭМЃЈ3ЃЉБШЭМЃЈ2ЃЉЖрГі5ИіЁАЪїжІЁБЃЌЭМЃЈ4ЃЉБШЭМЃЈ3ЃЉЖрГі10ИіЁАЪїжІЁБЃЌееДЫЙцТЩЃЌЭМЃЈ7ЃЉБШЭМЃЈ6ЃЉЖрГі_____ИіЁАЪїжІЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
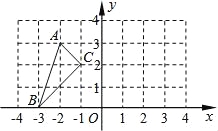
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФЖЅЕуЖМдкЗНИёЯпЕФНЛЕуЃЈИёЕуЃЉЩЯЃЎ
ЃЈ1ЃЉНЋЁїABCШЦCЕуАДФцЪБеыЗНЯђа§зЊ90ЁуЕУЕНЁїAЁфBЁфCЁфЃЌЧыдкЭМжаЛГіЁїAЁфBЁфCЁфЃЎ
ЃЈ2ЃЉНЋЁїABCЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌдйЯђгвЦНвЦ5ИіЕЅЮЛЕУЕНЁїAЁхBЁхCЁхЃЌЧыдкЭМжаЛГіЁїAЁхBЁхCЁхЃЎ
ЃЈ3ЃЉШєНЋЁїABCШЦдЕуOа§зЊ180ЁуЃЌAЕФЖдгІЕуA1ЕФзјБъЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
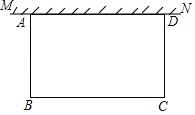
ЁОЬтФПЁПШчЭМЃЌдкзуЙЛДѓЕФПеЕиЩЯгавЛЖЮГЄЮЊaУзЕФОЩЧНMNЃЌФГШЫРћгУОЩЧНКЭФОРИЮЇГЩвЛИіОиаЮВЫдАABCDЃЌЦфжаADЁмMNЃЌвбжЊОиаЮВЫдАЕФвЛБпППЧНЃЌСэШ§БпвЛЙВгУСЫ100УзФОРИЃЎ
ЃЈ1ЃЉШєa=20ЃЌЫљЮЇГЩЕФОиаЮВЫдАЕФУцЛ§ЮЊ450ЦНЗНУзЃЌЧѓЫљРћгУОЩЧНADЕФГЄЃЛ
ЃЈ2ЃЉЧѓОиаЮВЫдАABCDУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуPЕФзјБъЮЊ(mЃЋ1ЃЌmЃ1)ЃЎ

(1)ЪдХаЖЯЕуPЪЧЗёдквЛДЮКЏЪ§yЃНxЃ2ЕФЭМЯѓЩЯЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЭМЃЌвЛДЮКЏЪ§yЃНЃ![]() xЃЋ3ЕФЭМЯѓгыxжсЁЂyжсЗжБ№ЯрНЛгкAЃЌBЃЌШєЕуPдкЁїAOBЕФФкВПЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
xЃЋ3ЕФЭМЯѓгыxжсЁЂyжсЗжБ№ЯрНЛгкAЃЌBЃЌШєЕуPдкЁїAOBЕФФкВПЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌABЃНACЃЌвдABЮЊжБОЖЕФЁбOЗжБ№гыBCЁЂACНЛгкЕуDЁЂEЃЌЙ§ЕуDзїЁбOЕФЧаЯпDFЃЌНЛACгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDFЁЭACЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ4ЃЌЁЯCDFЃН22.5ЁуЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯЕуAБэЪОЪ§aЃЌЕуCБэЪОЪ§cЃЌЧвЖрЯюЪНx3+15x2y2Љ20ЕФГЃЪ§ЯюЪЧaЃЌзюИпДЮЯюЕФЯЕЪ§ЪЧcЃЎЮвУЧАбЪ§жсЩЯСНЕужЎМфЕФОрРыгУБэЪОСНЕуЕФДѓаДзжФИвЛЦ№БъМЧЃЎБШШчЃЌЕуAгыЕуBжЎМфЕФОрРыМЧзїABЃЎ
ЃЈ1ЃЉЧѓaЃЌcЕФжЕЃЛ
ЃЈ2ЃЉЖЏЕуBДгЪ§Љ6ЖдгІЕФЕуПЊЪМЯђгвдЫЖЏЃЌЫйЖШЮЊУПУы2ИіЕЅЮЛГЄЖШЃЎЭЌЪБЕуAЃЌCдкЪ§жсЩЯдЫЖЏЃЌЕуAЃЌCЕФЫйЖШЗжБ№ЮЊУПУы3ИіЕЅЮЛГЄЖШЃЌУПУы4ИіЕЅЮЛГЄЖШЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЂйШєЕуAЯђгвдЫЖЏЃЌЕуCЯђзѓдЫЖЏЃЌABЃНBCЃЎЧѓtЕФжЕЃЛ
ЂкШєЕуAЯђзѓдЫЖЏЃЌЕуCЯђЪЏдЫЖЏЃЌ2ABЉmBCЕФжЕВЛЫцЪБМфtЕФБфЛЏЖјИФБфЃЌЧѓГіmЕФжЕЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com