
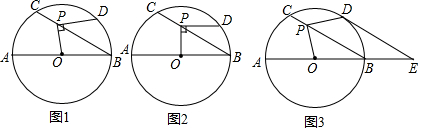
分析 (1)根据题意首先得出半径长,再利用锐角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
解答 解:(1)如图2,连接OD,
∵OP⊥PD,PD∥AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OB•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
在Rt△POD中,
PD=$\sqrt{O{D}^{2}-O{P}^{2}}$=$\sqrt{{6}^{2}-(2\sqrt{3})^{2}}$=2$\sqrt{6}$;
(2)①证明:如图3,连接OD,交CB于点F,连接BD,
∵$\widehat{DC}$=$\widehat{AC}$,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,
∵BE=$\frac{1}{2}$AB,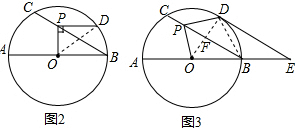
∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OB•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在Rt△POD中,OF=DF,
∴PF=$\frac{1}{2}$DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF-PF=3$\sqrt{3}$-3.
点评 此题主要考查了圆的综合以及直角三角形的性质和锐角三角三角函数关系,正确得出△OBD是等边三角形是解题关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
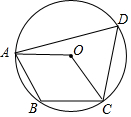 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
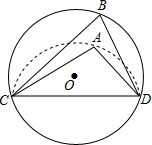 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )| A. | 110° | B. | 70° | C. | 60° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 地区 | A | B | C | D | E | F | G | H | I |
| 万册 | 28 | 24 | 23 | 14 | 16 | 15 | 5 |
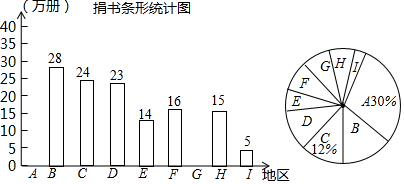
| A. | 捐书的总数为200万册 | |
| B. | 捐书数据的中位数是16万册 | |
| C. | 捐书数据的众数是60万册 | |
| D. | 捐书数扇形统计图中表示G的扇形的圆心角为30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,$\frac{17}{6}$) | B. | (4,3) | C. | (5,$\frac{17}{6}$) | D. | (5,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com