
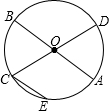
 如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.
如图,已知AB和CD是⊙O的两条直径,CE∥AB,若$\widehat{CE}$的度数为40°,则$\widehat{AE}$的度数为70°.  名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com