
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{2015}$ |
分析 利用平方差公式$\frac{{n}^{2}-1}{{n}^{2}}$=$\frac{(n+1)(n-1)}{{n}^{2}}$,对所求式子进行化简,从而进行求解.
解答 解:∵$\frac{{n}^{2}-1}{{n}^{2}}$=$\frac{(n+1)(n-1)}{{n}^{2}}$,
∴原式=$\frac{3×1}{{2}^{2}}$×$\frac{2×4}{{3}^{2}}$×$\frac{3×5}{{4}^{2}}$×…×$\frac{2015×2017}{201{6}^{2}}$=$\frac{1}{2}$×$\frac{2017}{2016}$
∴$\frac{({2}^{2}-1)({3}^{2}-1)({4}^{2}-1)…(201{5}^{2}-1)(201{6}^{2}-1)}{{1}^{2}•{2}^{2}•{3}^{2}•{4}^{2}…201{5}^{2}•201{6}^{2}}$的值应该最接近于$\frac{1}{2}$.
故选:B.
点评 此题主要考查平方差公式的性质及其应用,解题的关键是利用平方差公式进行展开.


科目:初中数学 来源: 题型:选择题
| A. | 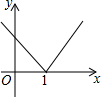 | B. | 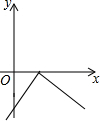 | C. | 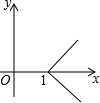 | D. | 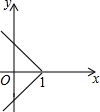 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
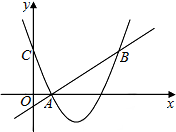 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com