
【题目】抛物线![]() ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线![]() 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线![]() 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线![]() 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
【答案】(1)证明见试题解析;(2)![]() ,或
,或![]() .
.
【解析】
试题(1)由“恒定”抛物线的定义,即可得出抛物线恒过定点(﹣1,0);
(2)求出抛物线![]() 的顶点坐标和B的坐标,由题意得出PA∥CQ,PA=CQ;存在两种情况:①作QM⊥AC于M,则QM=OP=
的顶点坐标和B的坐标,由题意得出PA∥CQ,PA=CQ;存在两种情况:①作QM⊥AC于M,则QM=OP=![]() ,证明Rt△QMC≌Rt△POA,MC=OA=1,得出点Q的坐标,设抛物线的解析式为
,证明Rt△QMC≌Rt△POA,MC=OA=1,得出点Q的坐标,设抛物线的解析式为![]() ,把点A坐标代入求出a的值即可;
,把点A坐标代入求出a的值即可;
②顶点Q在y轴上,此时点C与点B重合;证明△OQC≌△OPA,得出OQ=OP=![]() ,得出点Q坐标,设抛物线的解析式为
,得出点Q坐标,设抛物线的解析式为![]() ,把点C坐标代入求出a的值即可.
,把点C坐标代入求出a的值即可.
试题解析:(1)由“恒定”抛物线![]() ,得:b=a+c,即a﹣b+c=0,∵抛物线
,得:b=a+c,即a﹣b+c=0,∵抛物线![]() ,当x=﹣1时,y=0,∴“恒定”抛物线
,当x=﹣1时,y=0,∴“恒定”抛物线![]() 必过x轴上的一个定点A(﹣1,0);
必过x轴上的一个定点A(﹣1,0);
(2)存在;理由如下:∵“恒定”抛物线![]() ,当y=0时,
,当y=0时,![]() ,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=
,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=![]() ,∴顶点P的坐标为(0,
,∴顶点P的坐标为(0,![]() ),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,
),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,
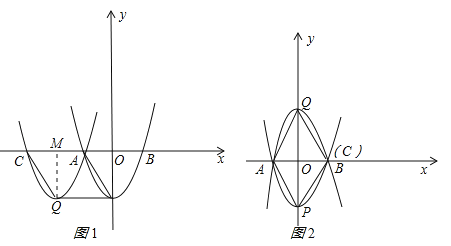
∴存在两种情况:①如图1所示:作QM⊥AC于M,则QM=OP=![]() ,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,∵CQ=PA,QM=OP,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,
,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,∵CQ=PA,QM=OP,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,![]() ),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为
),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为![]() ,把点A(﹣1,0)代入得:a=
,把点A(﹣1,0)代入得:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为:![]() ,即
,即![]() ;
;
②如图2所示:顶点Q在y轴上,此时点C与点B重合,∴点C坐标为(1,0),∵CQ∥PA,∴∠OQC=∠OPA,在△OQC和△OPA中,∵∠OQC=∠OPA,∠COQ=∠AOP,CQ=PA,∴△OQC≌△OPA(AAS),∴OQ=OP=![]() ,∴点Q坐标为(0,
,∴点Q坐标为(0,![]() ),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为
),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为![]() ,把点C(1,0)代入得:a=
,把点C(1,0)代入得:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为:![]() ;
;
综上所述:存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形,抛物线的解析式为:![]() ,或
,或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】杨梅是漳州的特色时令水果.杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价每件比第一批多了5元.
(1)第一批杨梅每件进价多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出![]() 后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润
后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润![]() 售价
售价![]() 进价)?
进价)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE=![]() ,求菱形BEDF的面积.
,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司营销A,B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系![]() 。
。
当x=1时,y=1.4;当x=3时,y=3.6。
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系![]() 。
。
根据以上信息,解答下列问题:
(1)求二次函数解析式;
(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
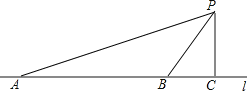
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
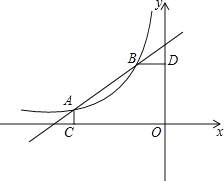
【题目】如图,在平面直角坐标系中,直线y=![]() x+
x+![]() 与反比例函数y=
与反比例函数y=![]() (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(1)求a 、b及k的值;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
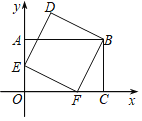
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com