
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于原点
轴交于原点![]() 和点
和点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)求![]() 的值;
的值;
(3)点![]() 在抛物线的对称轴上,如果
在抛物线的对称轴上,如果![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;对称轴为
;对称轴为![]() ;(2)2;(3)
;(2)2;(3)![]()
【解析】
(1)将点O(0,0),点B(4,0)分别代入使用待定系数法即可求得解析式,然后再使用对称轴公式解答即可;
(2)把点A(3,m)代入y=-x2+4x,求出m的值,得到点A的坐标,过点B作BM⊥OA,交OA于点M,过点A作AE⊥OB,交OB于点E,然后根据三角形的面积和勾股定理,求出线段BM和AM的长,最后运用正切的定义解答即可;
(3)把AB绕点B逆时针旋转90°得到BC,作AE⊥OB于E,CF⊥OB于F,CA交直线x=2于D点,利用△BAC为等腰直角三角形得到∠CAB=45°,证明△ABE≌△BCF得到BF=AE=3,BE=CF=1,则C(1,-1),根据待定系数法求出直线AC的解析式为y=2x-3,然后计算自变量为2对应的一次函数值,即可确定D点的坐标.
解:由待定系数法得:
![]() 解得
解得![]()
所以抛物线的表达式为:y=-x2+4x,它的对称轴为:x=![]()
(2)把点A(3,m)代入y=-x2+4x,解得m==3,则点A的坐标为(3,3)
如图:过点B作BM⊥OA,交OA于点M,过点A作AE⊥OB交OB于点E
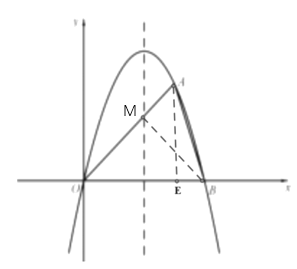
AE=3,OE=3,BE=4-3=1,OA=![]() , AB=
, AB=![]()
S△OAB=![]()
∴BM![]()
∴AM=![]()
∴![]()
(3)把AB绕点B逆时针旋转90°得到BC,如图所示,作AE⊥OB于E,CF⊥OB于F,CA交直线x=2于D点,
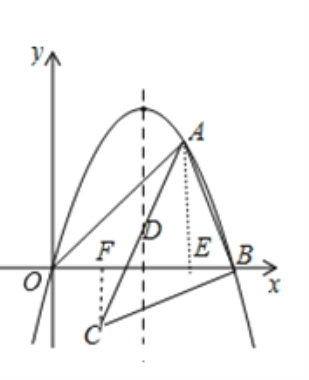
∵BA=BC,∠ABC=90°,
∴△BAC为等腰直角三角形
∴∠CAB=45°
∵∠ABE=∠BCF,∠AEB=∠BFC=90°
∴△ABE≌△BCF(AAS)
∴BF=AE=3,BE=CF=1
∴C(1,-1)
∴直线AC的解析式为y=2x-3,
∴当x=2时D点坐标为(2,1)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一批水果,平均每天可售出![]() ,每千克盈利
,每千克盈利![]() 元,经调查发现,每千克降价
元,经调查发现,每千克降价![]() 元,商店平均每天可多售出
元,商店平均每天可多售出![]() 水果,则商店平均每天的最高利润为______________ 元
水果,则商店平均每天的最高利润为______________ 元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,那么EE1的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为多少步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此,某校随机抽取了九年级(一)班的学生对安全知识的了解情况进行了一次调查统计图1和图2是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
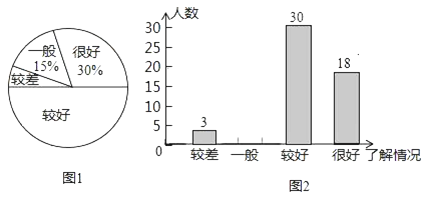
(1)此次调查共抽查了________名学生;
(2)补全统计图;
(3)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是________;
(4)若全校有1800名学生,估计对安全知识的了解情况为“很好”的学生共有________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.
(1)用含m的代数式表示点A、B的坐标;
(2)求证:![]() ;
;
(3)若点C、点A到y轴的距离相等,且s△CDE=1.6时,求抛物线和直线BE的解析式.
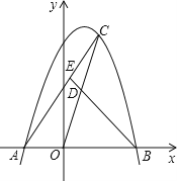
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com