
����Ŀ��ij�̳���������С���������д������������һ����������ת����ת�̽���ҡ��������涨�˿�ÿ����200Ԫ��Ʒ���Ϳ��Ի��һ��ת��ת�̵Ļ��ᣬС�����ݻ���������һ������ͳ��ͼ����ͼ��ʾ��
��1����ÿת��һ��ת������ù���ȯ����ƽ������
��2��С������һ��ʵ�飬��ת��200��ת�̣��ܹ����5800Ԫ����ȯ����ƽ��ÿת��һ��ת�̻�õĹ���ȯ�Ƕ���Ԫ��
��3������˵�������������Ϊʲô�в��

���𰸡���1��26Ԫ����2��29Ԫ����3������ģ��ʵ�鲻���ڸ��ʣ�ֻ���������ε�����»�ӽ����ʣ����������ݲ�ͬ��
�������������������1����������ͼ��ʾ����ù���ȯ���������ƽ�������ɣ�
��2��������ת��200��ת�̣��ܹ����5800Ԫ����ȯ��5800��200���ɵó�ƽ��ÿת��һ��ת�̻�õĹ���ȯ��
��3������ģ��ʵ������ʵĶ��弴�ɵó��𰸣�
�����������1����������ͼ�ɵó�����100��10%+50��20%+20��30%����1=26��Ԫ����
��ÿת��һ��ת������ù���ȯ����ƽ����Ϊ26Ԫ��
��2������ת��200��ת�̣��ܹ����5800Ԫ����ȯ��
����ƽ��ÿת��һ��ת�̻�õĹ���ȯ��![]() =29��Ԫ����
=29��Ԫ����
��3������ģ��ʵ�鲻���ڸ��ʣ�ֻ���������ε�����»�ӽ����ʣ����������ݲ�ͬ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]()
��1��ֻ����ֱ�ߺ����dzߣ���C����CD��AB����������ͼ�ۼ���
��2��˵��![]() �����ɣ�
�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��鷽ʽ������Ϊ����ʵ��ǣ� ��
A.Ϊ���˽�ͬѧ�Ƕ����ӡ������˴�������Ŀ��ϲ���̶ȣ�С����ѧУ����ɷ���![]() �����꼶ѧ��
�����꼶ѧ��
B.�����������ÿ��Ϸɻ����а��죬���ó������鷽ʽ
C.Ϊ���˽����������꼶ѧ�����������������ȫ����鷽ʽ
D.Ϊ���˽���ʡ�������ƽ���õ��������ó������鷽ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ô����������ϱ�ʾ��һ������Χ�����������Χ���������д���1��С��2������������1��2���������ĵ���ģ���ʾ�����Χ��������1��2����

�����������ϱ�ʾ��һ����Χ��ʹ�������Χ��
��1���������д��ک�3��С��0�������������ᣨ1���ϣ���
��2��������1.5����������������ֻ����5���������������ᣨ2���ϣ���
��3��ͬʱ���������������������������ᣨ3���ϣ�
��������100�Ի�Ϊ�෴����100�Ի�Ϊ������
����������������
�������Χ������������С������ʾ�ĵ�ľ������3��С��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�Ǿ���ABCD�ı�CD��һ�㣬����ADE��AE���ۣ���D�ĶԳƵ�Fǡ������BC�ϣ���֪�ۺ�AE=![]() cm����tan��EFC=
cm����tan��EFC=![]() ����ô�þ��ε��ܳ�Ϊ________��
����ô�þ��ε��ܳ�Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
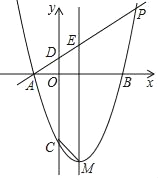
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2+bx+c�ĶԳ���Ϊֱ��x=1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����AB=4����P����������λ�ڵ�һ���ĵ㣬ֱ��AP��y�ύ�ڵ�D����Գ��ύ�ڵ�E�����P�ĺ�����Ϊt��
��1�����A������������ߵı���ʽ��
��2����AE��EP=1��2ʱ�����E�����ꣻ
��3���������ߵĶ���ΪM����y��Ľ���ΪC�����ı���CDEM�ǵ�������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�����Ϊ20cm2���Խ��߽��ڵ�O����AB��AOΪ�ڱ���ƽ���ı���AOC1B���Խ��߽��ڵ�O1����AB��AO1Ϊ�ڱ���ƽ���ı���AO1C2B���������ƣ���ƽ���ı���AO2019C2020B�����Ϊ��������cm2��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߿Ƽ�������ʶ������ij��ѧ�ڡ�2016��Ƽ��ڡ���о��пƼ���������������ģ�����������ˡ�����������������ģ���ĸ����ÿ��ѧ��ֻ�ܲμ�һ�����ı�������������������ͳ����ͼ��

�����������Ϣ������������⣺
��1��ȫ�������ѧ������ �ˣ�����ģ��������ͳ��ͼ�е�Բ�Ľ��� �㣻
��2��������ͳ��ͼ����������
��3���ڱ�������У���á���������һ�Ƚ���ѧ��Ϊ1��������2��Ů������á���ģ����һ�Ƚ���ѧ��Ϊ1��������1��Ů�����ִ���������һ�Ƚ���ѧ���и����ѡȡ1��ѧ���μ��м���������ģ����������ѡȡ��������ǡΪ1����1Ů���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߳�Ϊ2��������ABCD��E��AB���е�,P������DC�ϴ�D������ÿ��1����λ���ȵ��ٶ��˶�,��P��PF��DE,���˶�ʱ��Ϊ__________��ʱ���Ե�P��F��EΪ���������������AED����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com