
【题目】甲、乙两人从学校出发,沿相同的线路跑向公园.甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(3)乙出发 秒后与甲第一次相遇.

【答案】(1)900,1.5;(2)2.5,100;(3)150
【解析】
(1)根据函数图象可以得到甲跑的路程和甲的速度;
(2)根据函数图象和题意,可以得到乙跑步的速度及乙在途中等候甲的时间;
(3)根据函数图象可以分别求得甲乙的函数关系式,然后联立组成二元一次方程组,即可解答本题
解:(1)有函数图象可得,
在跑步的全过程中,甲共跑了900米,甲的速度为:900÷600=1.5米/秒,
故答案为:900,1.5;
(2)由图象可得,
甲跑500秒的路程是:500×1.5=750米,
甲跑600米的时间是:(750﹣150)÷1.5=400秒,
乙跑步的速度是:750÷(400﹣100)=2.5米/秒,
乙在途中等候甲的时间是:500﹣400=100秒,
即乙跑步的速度是2.5米/秒,乙在途中等候甲的时间是100秒;
(3)∵D(600,900),A(100,0),B(400,750),
∴OD的函数关系式是y=1.5x,
设AB的函数关系式是:y=kx+b,
∴![]() ,解得
,解得![]()
∴y=2.5x﹣250,
根据题意得,![]()
解得x=250,
250﹣100=150(秒),
即乙出发150秒时第一次与甲相遇.
故答案为:(1)900;1.5;(2)2.5;100;(3)150.


科目:初中数学 来源: 题型:
【题目】记面积为18cm2的平行四边形的一条边长为x(cm),这条边上的高线长为y(cm).
(1)写出y关于x的函数表达式及自变量x的取值范围;
(2)在如图直角坐标系中,用描点法画出所求函数图象;
(3)若平行四边形的一边长为4cm,一条对角线长为![]() cm,请直接写出此平行四边形的周长.
cm,请直接写出此平行四边形的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《中华人民共和国个人所得税法》,新个税标准将于2019年1月1日起施行.其中每月纳税的起征点增加到5000元,即2019年1月以后每月工资中的5000元将不必缴纳税款.根据相关政策,纳税部门给大家制作了如下纳税表格(未完整):
级数 | 全月应纳税所得额(含税级距) | 税率( | 速算扣除数 |
1 | 不超过3000元的部分 |
| 0 |
2 | 超过3000元至12000元的部分 |
| 210 |
3 | 超过12000元至25000元的部分 |
| 1410 |
4 | 超过25000元至35000元的部分 |
|
|
5 | 超过35000元至55000元的部分 |
| 4410 |
6 | 超过55000元至80000元的部分 |
| 7160 |
7 | 超过80000元的部分 |
| 15160 |
例如:张三2019年1月如果月收入为21000元,则他1月中的![]() 元应该纳税,纳税数额为:
元应该纳税,纳税数额为:![]() (元).
(元).
(1)如果李士业2019年1月份收入为7000元,则他1月份应纳税多少元?
(2)如果王努利2019年1月份收入为10000元,则他月份应纳税多少元?
(3)钱勒凤跟朋友说,估计自己1月份应纳税3400元,则钱勤奋1月份收入约有多少元?
(4)根据表中各数据关系,求表格中的![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ![]() ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( ) 
A.(3,2)
B.(3,1)
C.(2,2)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于( )
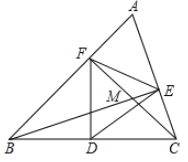
A. 14B. 13C. 12D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x= ![]() 与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<
与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x< ![]() 时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )
时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )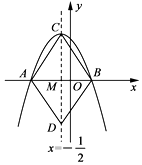
A.②③④
B.①②③
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com