
��ͼ���ھ���OABC�У���A��0��10����C��8��0��.��ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC�� OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ�������� ����O��D��C���㣮
����O��D��C���㣮

��1����D�ĵ����꼰�����ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ��������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
��1��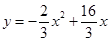 ����2��
����2��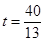 ��
�� ����3�����ڷ���������M��N�㣬�����ǵ�����Ϊ����M1����4����32����N1��4����38������M2��12����32����N2��4����26������M3��4��
����3�����ڷ���������M��N�㣬�����ǵ�����Ϊ����M1����4����32����N1��4����38������M2��12����32����N2��4����26������M3��4�� ����N3��4��
����N3��4�� ����
����
��������
�����������1�������۵�ͼ�ε���Գ��ԣ���CED����CBDȫ�ȣ�������Rt��CEO�����OE�ij��������ɵõ�AE�ij�����Rt��AED�У�AD=AB��BD��ED=BD�����ù��ɶ��������AD�ij�����һ����ȷ��D�����꣬���ô���ϵ����������������ߵĽ���ʽ��
��2�����ڡ�DEC=90�㣬������ȷ�����ǡ�AED=��OCE������P��Q��CΪ��������������ADE���ƣ���ô��QPC=90����PQC=90�㣬Ȼ��������������£��ֱ��������������εĶ�Ӧ�߳ɱ��������Ӧ��t��ֵ��
��3��������M��N��C��EΪ������ı��Σ��ߺͶԽ��߶�û��ȷָ��������Ҫ������������ۣ���EC��ƽ���ı��εĶԽ��ߣ���ôEC��MN�ػ���ƽ�֣�����EC���е������������߶Գ����ϣ�����M��һ���������ߵĶ��㣻
��EC��ƽ���ı��εıߣ���ôEC��MNƽ������ȣ����������N�����꣬Ȼ����E��C�ĺᡢ��������ʾ��M�����꣬�ٽ���M���������ߵĽ���ʽ�У�����ȷ��M��N�����꣮
�����������1�����ı���ABCOΪ���Σ����OAB=��AOC=��B=90�㣬AB=CO=8��AO=BC=10�������⣬��BDC�ա�EDC�����B=��DEC=90�㣬EC=BC=10��ED=BD���ɹ��ɶ�����EO=6����AE=10��6=4����AD= ����BD=ED=
����BD=ED=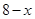 ���ɹ��ɶ�������
���ɹ��ɶ������� ����ã�
����ã� ����AD=3����������
����AD=3���������� ����D��3��10����C��8��0����O��0��0����
����D��3��10����C��8��0����O��0��0���� �����
����� ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ��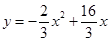 ��
��
��2���ߡ�DEA+��OEC=90�㣬��OCE+��OEC=90�㣬���DEA=��OCE���ɣ�1���ɵ�AD=3��AE=4��DE=5����CQ=t��EP=2t����PC=10��2t���ٵ���PQC=��DAE=90�㣬��ADE�ס�QPC���� =
= ����
���� �����
�����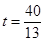 ���ڵ���QPC=��DAE=90�㣬��ADE�ס�PQC����
���ڵ���QPC=��DAE=90�㣬��ADE�ס�PQC���� =
= ����
���� �����
����� ���൱
���൱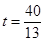 ��
�� ʱ����P��Q��CΪ��������������ADE���ƣ�
ʱ����P��Q��CΪ��������������ADE���ƣ�

��3��������ڷ���������M��N�㣬������������ۣ���ECΪƽ���ı��εĶԽ��ߣ����������ߵĶԳ��ᾭ��EC�е㣬���ı���MENC��ƽ���ı��Σ���ôM���Ϊ�����߶��㣻
��M��4�� ������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4��
������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4�� ����
����
��ECΪƽ���ı��εıߣ���EC MN����N��4��m������M��4��8��m+6����M��4+8��m��6����
MN����N��4��m������M��4��8��m+6����M��4+8��m��6����
��M����4��m+6�����������ߵĽ���ʽ�У��ã�m=��38����ʱ N��4����38����M����4����32����
��M��12��m��6�����������ߵĽ���ʽ�У��ã�m=��26����ʱ N��4����26����M��12����32����
���ϣ����ڷ���������M��N�㣬�����ǵ�����Ϊ����M1����4����32����N1��4����38������M2��12����32����N2��4����26������M3��4�� ����N3��4��
����N3��4�� ����
����

���㣺1�����κ����ۺ��⣻2�������ͣ�3���������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
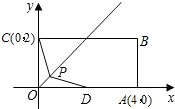 ����ʱ��P������͡�PDE���ܳ���
����ʱ��P������͡�PDE���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
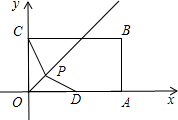 ƽ�����ϵ�һ�����㣨�����O�غϣ���
ƽ�����ϵ�һ�����㣨�����O�غϣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | x |
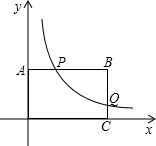 AB���е㣬���P�ĺ�����Ϊa��
AB���е㣬���P�ĺ�����Ϊa���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
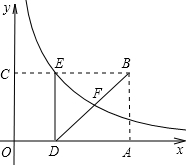 ��2012•�����ʼ죩��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x�ᡢy����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������y=
��2012•�����ʼ죩��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x�ᡢy����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 3 |
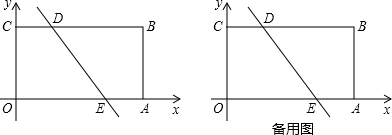
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com