
【题目】已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数![]() 图象的两个交点.
图象的两个交点.
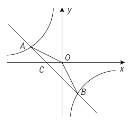
(1)求一次函数和反比例函数的解析式.
(2)求![]() 的面积.
的面积.
(3)观察图象,直接写出不等式![]() 的解集.
的解集.
【答案】(1)一次函数解析式为:y=-x-2;反比例函数解析式为:![]() ;(2)6;(3)x<-4或0<x<2
;(2)6;(3)x<-4或0<x<2
【解析】
(1)先把点A的坐标代入反比例函数解析式,即可得到m=-8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;(2)先求出直线y=-x-2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;(3)观察函数图象得到当x<-4或0<x<2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
解:

把A(-4,2)代入y=![]() ,得m=2×(-4)=-8,
,得m=2×(-4)=-8,
所以反比例函数解析式为y=![]() ,
,
把B(n,-4)代入y=![]() ,得-4n=-8,
,得-4n=-8,
解得n=2,
把A(-4,2)和B(2,-4)代入y=kx+b,得![]() ,
,
解得![]() ,
,
所以一次函数的解析式为y=-x-2;
(2)y=-x-2中,令y=0,则x=-2,
即直线y=-x-2与x轴交于点C(-2,0),
∴S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×4=6;
×2×4=6;
(3)由图可得,不等式kx+b-![]() >0的解集为:x<-4或0<x<2.
>0的解集为:x<-4或0<x<2.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场销售某种款式童装,一天可售出30套,每套盈利40元.为了扩大销售,增加盈利,商场决定采取降价措施.若一套童装每降价1元,平均每天可多售出2套,设每套童装降价![]() 元时,商场一天可获利润
元时,商场一天可获利润![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)若要商场每天盈利1500元,则应降价多少元?
(3)当每套童装降价多少元时,商场可获最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
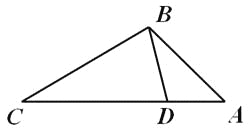
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
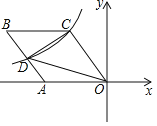
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)如图所示,下列结论:①abc<0;②点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2;③b2>(a+c)2;④2a﹣b<0.正确的结论有( )
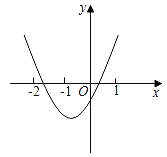
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
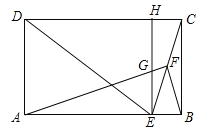
【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
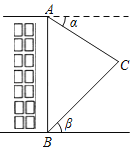
【题目】如图,建筑物AB的高为52米,在其正前方广场上有人进行航模试飞.从建筑物顶端A处测得航模C的俯角α=30°,同一时刻从建筑物的底端B处测得航模C的仰角β=45°,求此时航模C的飞行高度.(精确到1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com