练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．一个正方形的边长增加了2cm，面积相应增加了28cm2，则这个正方形的边长为6cm．

    分析 设这个正方形的边长为xcm，根据题意列出方程，求出方程的解即可得到结果．

    解答 解：设这个正方形的边长为xcm，
    根据题意得：（x+2）2-x2=28，
    整理得：4x+4=28，
    解得：x=6，
    则这个正方形的边长为6cm，
    故答案为：6

    点评 此题考查了完全平方公式的几何背景，熟练掌握完全平方公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

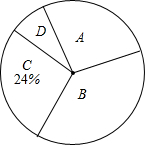    13．某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A，B，C，D四类，其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：
    类别ABCD
    频数304024b
    频率a0.40.240.06
    （1）表中的a=0.3，b=6；
    （2）根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；
    （3）若该校有学生1000名，根据调查结果估计该校学生中类别为D的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，在等腰直角三角形ABC中，∠ABC=90°，AB=BC=2，P是△ABC所在平面内一点，且满足PA⊥PB，则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2016个点的坐标为（45，9）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．已知x2+kx+16是一个完全平方式，则k的值为（　　）
    A．4B．8C．-8D．±8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．将一副三角尺按如图所示的方式叠放在一起，边AB与CD相交于点E，则$\frac{DE}{EC}$的值等于$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

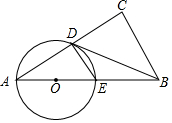    5．如图，在Rt△ABC中，∠C=90°，点D是AC的中点，过点A、D作⊙O，⊙O与AB交于点E，AE是⊙O的直径，AD是⊙O的一条弦，且∠A+∠CDB=90°，AD：AE=4：5，BC=6．
    （1）求证：直线BD与⊙O相切；
    （2）下面是根据题中条件求直径AE长的过程，阅读后请按要求解决下列问题：
    解法1．∵AE是⊙O的直径，∴∠ADE=90°=∠C，∴DE∥BC
    又∵D是AC的中点，∴$\frac{AE}{AB}$=$\frac{DE}{BC}$=$\frac{1}{2}$=$\frac{AD}{AC}$，∴E是AB的中点，∴DE=$\frac{1}{2}$BC=3．
    在Rt△ADE中，设AD=4x，AE=5x，∴（4x）2+32=（5x）2，
    解之得：x1=1，x2=-1（舍去），∴AE=5x=5，即⊙O的直径为5．
    解法2．∵∠A+∠CDB=90°，又∵∠A+∠CBA=90°，∴∠CDB=∠CBA，∠C=∠C，
    ∴△DCB∽△BCA，∴$\frac{DC}{BC}$=$\frac{BC}{AC}$，∴BC2=DC•AC，又∵AC=2DC=2AD，∴BC2=AD•2AD，
    AD=$\frac{4}{5}$AE，62=2×（$\frac{4}{5}$AE）2，AE=$\frac{15}{4}$$\sqrt{2}$．
    以上两种解法结果不同，那么问题出在哪里呢？
    ①下列说法正确的是D
    A．解法1有错     B．解法2有错     C．解法1、2都有错    
    D．解法1、2都没错，但题中条件“AD：AE=4：5”是多余的
    ②在①中若你选择的是A、B、C中一个，请说明错在哪里？若你选的是D，请删去“AD；AE=4：5”这个条件，求出⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某公司开发出一种高科技电子节能产品，投资2500万元一次性购买整套生产设备，此外生产每件产品需成本20元，每年还需投入500万广告费，按规定该产品的售价不得低于30元/件且不得高于70元/件，该产品的年销售量y（万件）与售价x（元/件）之间的函数关系如下表：
     x（元/件） 30 31… 70
     y（万件） 120 119… 80
    （1）求y与x的函数关系式，并写出x的取值范围；
    （2）第一年公司是盈利还是亏损？并求出当盈利最大或亏损最小时该产品的售价；
    （3）在（2）的前提下，即在第一年盈利最大或亏损最小时，第二年公司重新确定产品定价，能否使两年盈利3500万元？若能，求第二年产品的售价；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．有四根细木棒，长度分别为 3cm、5cm、7cm、9cm，以其中任意三条为边可以构成3个三角形．

    查看答案和解析>>

    同步练习册答案