
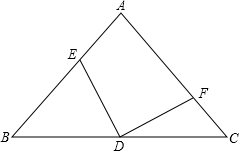
 如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若BC=4,求四边形AEDF的面积.
如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若BC=4,求四边形AEDF的面积. 分析 先连接AD,根据等腰直角三角形的性质,求得AD=CD=2,∠DAE=∠C=45°,∠ADE=∠CDF,进而判定△ADE≌△CDF,得出四边形AEDF的面积=△ACD的面积即可.
解答 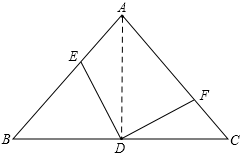 解:连接AD,
解:连接AD,
∵∠A=90°,AB=AC,D为边BC中点,BC=4,
∴AD⊥BC,AD=CD=2,∠DAE=∠C=45°,
∴∠ADE+∠ADF=∠CDF+∠ADF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠DAE=∠C}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△ADE≌△CDF(ASA),
∴△ADE的面积=△CDF的面积,
∴四边形AEDF的面积=△ACD的面积=$\frac{1}{2}$×2×2=2.
点评 本题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质,解决问题的关键是作辅助线构造全等三角形,将四边形AEDF的面积转化为△ACD的面积.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com