
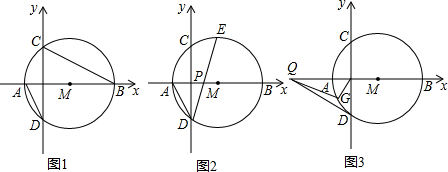
���� ��1����ͼ1�����ݶԶ�����ȵõ���AOD=��COB������Բ�ܽǶ����õ���ADO=��OBC������жϡ�AOD�ס�COB��
��2������AE��BE��MD����ͼ2���ȼ����OD=2�������ù��ɶ��������OD=4��AD=2$\sqrt{5}$������֤����PBE�ס�PDA���������Ʊȿɼ����BE=3$\sqrt{5}$��Ȼ����ݹ��ɿɼ����AE=$\sqrt{55}$�����������еĶ���õ�tan��ABE=$\frac{\sqrt{11}}{3}$�����ǵõ�tan��EDA=$\frac{\sqrt{11}}{3}$��
��3����ͼ3������MD��MG���������ߵ����ʵá�MDQ=90�㣬�ɡ�ODM=��OQD������ж�Rt��ODM��Rt��OQD���������Ʊȿɼ����OQ=$\frac{16}{3}$��
���ۣ���G����A���غ�ʱ����$\frac{OG}{QG}=\frac{OA}{AQ}=\frac{3}{5}$����G����B���غ�ʱ��$\frac{OG}{QG}=\frac{3}{5}$��
��G�㲻��A��B�غ�ʱ����֤����MOD�ס�MDQ�õ���MD2=MO•MQ������MD=MG����MG2=MO•MQ�����ϡ�OMG=��GMQ������жϡ�MOG�ס�MGQ���������Ʊȿɵ�$\frac{OG}{QG}=\frac{OM}{MG}=\frac{3}{5}$�����ǵõ�$\frac{GO}{GQ}$��ֵ���䣬��ֵ$\frac{3}{5}$��
��� ��1��֤������ͼ1��
�ߡ�AOD=��COB����ADO=��OBC��
���AOD�ס�COB��
��2���⣺����AE��BE��MD����ͼ2��
�ߵ�M������Ϊ��3��0����MA=MB=MD=5��
��OD=2��
��Rt��ODM��OD=$\sqrt{M{D}^{2}-O{M}^{2}}$=4��
��Rt��OAD��AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=2$\sqrt{5}$��
�ߡ�PEB=��PAD����PBE=��PDA��
���PBE�ס�PDA��
��$\frac{BE}{AD}=\frac{PB}{PD}=\frac{3}{2}$��
��BE=$\frac{3}{2}$��2$\sqrt{5}$=3$\sqrt{5}$��
��Rt��ABE��
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{55}$��
��tan��ABE=$\frac{AE}{BE}=\frac{\sqrt{55}}{3\sqrt{5}}=\frac{\sqrt{11}}{3}$��
�ߡ�EDA=��ABE��
��tan��EDA=$\frac{\sqrt{11}}{3}$��
��3���⣺$\frac{GO}{QG}$��ֵ���䣬��ֵ$\frac{3}{5}$��
�������£���ͼ3������MD��MG��
��DQΪ���ߣ�
��MD��QD��
���MDQ=90�㣬
�ߡ�ODM=��OQD��
��Rt��ODM��Rt��OQD��
��OD��OQ=OM��OD����4��OQ=3��4��
��OQ=$\frac{16}{3}$��
��G����A���غ�ʱ��$\frac{OG}{QG}=\frac{OA}{AQ}=\frac{2}{\frac{16}{3}-2}$=$\frac{3}{5}$��
��G����B���غ�ʱ��$\frac{OG}{QG}=\frac{OB}{BQ}=\frac{3}{5}$��
��G�㲻��A��B�غ�ʱ��
�ߡ�OMD=��DMQ��
���MOD�ס�MDQ��
��$\frac{MO}{MD}=\frac{MD}{MQ}$����MD2=MO•MQ��
��MD=MG��
��MG2=MO•MQ��
�ߡ�OMG=��GMQ��
���MOG�ס�MGQ��
��$\frac{OG}{QG}=\frac{OM}{MG}=\frac{3}{5}$��
����������$\frac{GO}{QG}$��ֵ���䣬��ֵ$\frac{3}{5}$��
���� ������Բ���ۺ��⣬��Ҫ���������������ε��жϺ����ʣ�Բ�ܽǶ��������ߵ����ʣ����ɶ�����֪ʶ�㣻���2���Ĺؼ��������AE��BE�����3���Ĺؼ���֤��Rt��ODM��Rt��OQD�͡�MOD�ס�MDQ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʱ��/t��min�� | 1 | 2.5 | 5 | 10 | 20 | 50 | �� |
| ·��/s��km�� | 2 | 5 | 10 | 20 | 40 | 100 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
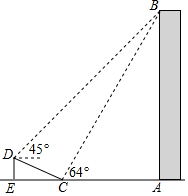 ��ͼ���ڴ�¥AB����ǰ����һб��CD��Ϊ13�ף��¶�Ϊ1��$\frac{12}{5}$����ΪDE����б�µĵ�C�����¥��B������Ϊ64�㣬��б�¶��ĵ�D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ���б�µĸ� DE���¥AB�ĸ߶ȣ����ο����ݣ�sin64���0.9��tan64���2��
��ͼ���ڴ�¥AB����ǰ����һб��CD��Ϊ13�ף��¶�Ϊ1��$\frac{12}{5}$����ΪDE����б�µĵ�C�����¥��B������Ϊ64�㣬��б�¶��ĵ�D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ���б�µĸ� DE���¥AB�ĸ߶ȣ����ο����ݣ�sin64���0.9��tan64���2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
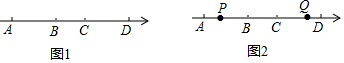 ��A��B��C��D�������ϵ�λ����ͼ1��ʾ����֪AB=3��BC=2��CD=4��
��A��B��C��D�������ϵ�λ����ͼ1��ʾ����֪AB=3��BC=2��CD=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 32017 | D�� | -32017 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{6x}{2y}$ | B�� | $\frac{x-1}{{x}^{2}}$ | C�� | $\frac{{x}^{2}+x}{x}$ | D�� | $\frac{x-1}{{x}^{2}-1}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com