分析:
(1)因为原方程有两个相等的实数根,故判别式△=(p+q+1)2-4p=(p+q-1)2+4q≥0,且α+β=p+q+1,αβ=p,于是p=αβ,q=α+β-p-1=α+β-αβ-1;
(2)因为α≤β,故只需求(1-a)(1-β)≤0即可;
(3)先根据条件确定动点所在的边,再确定点的坐标。
解答:
(1)∵α、β为方程x2-(p+q+1)x+p=0(q≥0)的两个实数根,
∴判别式△=(p+q+1)2-4p=(p+q-1)2+4q≥0,
且α+β=p+q+1,αβ=p,
于是p=αβ,
q=α+β-p-1=α+β-αβ-1;
(2)∵(1-a)(1-β)=1-(α+β)+αβ=-q≤0(q≥0),
又α≤β,
∴a≤1≤β;
(3)若使p+q=5/4
成立,只需α+β=p+q+1=9/4,
①当点M(α,β)在BC边上运动时,
由B(1/2,1),C(1,1),
得1/2≤α≤1,β=1,
而α=9/4-β=9/4-1=5/4>1,
故在BC边上存在满足条件的点,其坐标为(5/4,1)所以不符合题意舍去;
即在BC边上不存在满足条件的点。
②当点M(α,β)在AC边上运动时,
由A(1,2),C(1,1),
得a=1,1≤β≤2,
此时β=9/4-α=9/4-1=5/4,
又因为1<5/4<2,
故在AC边上存在满足条件的点,其坐标为(1,5/4);
③当点M(α,β)在AB边上运动时,
由A(1,2),B(1/2,1),
得1/2≤α≤1,1≤β≤2,
由平面几何知识得(1-α)/(1-1/2)=(2-β)/(2-1),
于是β=2α,
由β=2α且α+β=9/4
解得α=3/4,β=3/2,
又因为1/2<3/4<1,1<3/2<2,
故在AB边上存在满足条件的点,其坐标为(3/4,3/2)。
综上所述,当点M(α,β)在△ABC的三条边上运动时,存在点(1,5/4)和点(3/4,3/2),使p+q=5/4成立。
点评:此题较复杂,将根与系数的关系、根的判别式与动点问题相结合,体现了运动变化的观点.由于情况较多,需要分类讨论。

 的方程
的方程 的两实根为
的两实根为 ,且
,且 .
. 的代数式表示
的代数式表示 和
和 ;
; ;
; 为坐标的点
为坐标的点 在△ABC的三边上运动,且△ABC顶点的坐标分别为A
在△ABC的三边上运动,且△ABC顶点的坐标分别为A ,B
,B ,C
,C ,问是否存在点M,使
,问是否存在点M,使 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.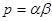 ,
,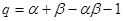
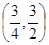 ;
;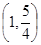


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案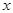 .试列出关于
.试列出关于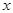 的方程: .
的方程: .