
【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
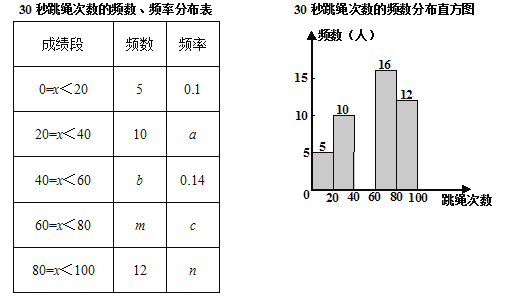
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
科目:初中数学 来源: 题型:
【题目】废旧电池是危险的固体废弃物之一,如果处理不当,不但会严重污染土壤和水源,还将直接危害人体健康. 一粒纽扣电池可使6×105kg水受到污染,相当于一个人一生的饮水量!我国每年约有8000万粒纽扣电池报废,如果处理不当,每年将会有多少水受到污染(请用科学记数法表示)?
查看答案和解析>>
科目:初中数学 来源: 题型:
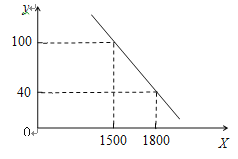
【题目】商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
(1)请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);
(2)若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为( )
A. 6,3,1 B. 3,6,1 C. 2,1,3 D. 2,3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
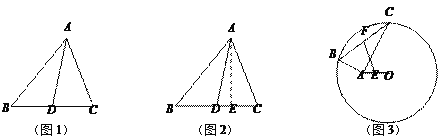
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
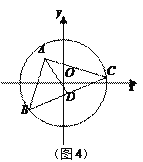
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年要实现大病保险全覆盖,中央财政安排城乡医疗救助补助资金160亿元,160亿元这一数据用科学记数法表示为( )
A.16×109元
B.1.6×1010元
C.0.16×1011元
D.1.6×109元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com