
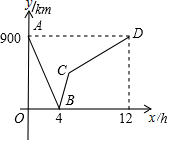
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究:分析 (1)根据已知条件和函数图象可以直接写出甲、乙两地之间的距离;
(2)根据题意可以得到点B表示的实际意义;
(3)根据图象和题意可以分别求出慢车和快车的速度;
(4)根据题意可以求得点C的坐标,由图象可以得到点B的坐标,从而可以得到线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围.
解答 解:(1)由图象可得,
甲、乙两地之间的距离为900km,
故答案为:900;
(2)图中点B的实际意义时当两车出发4小时时相遇;
(3)由题意可得,
慢车的速度为:900÷12=75km/h,
快车的速度为:(900-75×4)÷4=150km/h,
即慢车的速度是75km/h,快车的速度是150km/h;
(4)由题可得,
点C是快车刚到达乙地,
∴点C的横坐标是:900÷150=6,纵坐标是:900-75×6=450,
即点C的坐标为(6,450),
设线段BC对应的函数解析式为y=kx+b,
∵点B(4,0),点C(6,450),
∴$\left\{\begin{array}{l}{4k+b=0}\\{6k+b=450}\end{array}\right.$,得$\left\{\begin{array}{l}{k=225}\\{b=-900}\end{array}\right.$,
即线段BC所表示的y与x之间的函数关系式是y=225x-900(4≤x≤6).
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答,注意最后要写出自变量x的取值范围.


科目:初中数学 来源: 题型:填空题
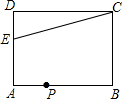 如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6.
如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+3)2+3 | B. | y=(x+3)2-1 | C. | y=(x-3)2+3 | D. | y=(x-3)2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x-1}$中x≠0 | B. | y=x2中x取全体实数 | ||
| C. | y=$\frac{1}{x+1}$中x≠-1 | D. | y=$\sqrt{x-1}$中x≥1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com