
分析 (1)根据题意,可以分别表示出方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)根据(1)中的函数解析式,将x=2200代入,求出相应的函数值,然后再比较大小,即可解答本题;
(3)根据(1)中的函数解析式可以分别求得用20000元,两种方案各购买多少苹果,然后比较大小,即可解答本题.
解答 解:(1)由题意可得,
方案A购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式:y=5.8x,
方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式:y=5x+2000;
(2)当x=2200时,
方案A:y=5.8×2200=12760(元),
方案B:y=5×2200+2000=13000(元),
∵12760<13000,
∴方案A付款少;
(3)由题意可得,
方案A可以购买的苹果数量为:20000÷5.8≈3448(kg),
方案B可以购买的苹果数量为:(20000-2000)÷5=3600(kg),
∵3600>3448,
∴他应选择方案B购买.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用函数的性质解答.


科目:初中数学 来源: 题型:解答题
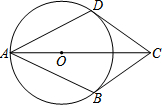 如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.
如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com