
【题目】若△ABC中AB=AC,且面积为定值,点P在直线BC上,且P到直线AC的距离为PF.当PF=3,C到AB的距离CH=7时,P到AB的距离为_____.
【答案】10或4.
【解析】
分两种情况讨论,由三角形的面积公式可求解.
如图①,
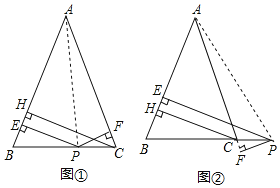
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴S△ABP=![]() ABPE,S△ACP=
ABPE,S△ACP=![]() ACPF,S△ABC=
ACPF,S△ABC=![]() ABCH.
ABCH.
又∵S△ABP+S△ACP=S△ABC,
∴![]() ABPE+
ABPE+![]() ACPF=
ACPF=![]() ABCH.
ABCH.
∵AB=AC,
∴PE+PF=CH,
∴PE=7﹣3=4;
如图②,PE=PF+CH.证明如下:
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴S△ABP=![]() ABPE,S△ACP=
ABPE,S△ACP=![]() ACPF,S△ABC=
ACPF,S△ABC=![]() ABCH,
ABCH,
∵S△ABP=S△ACP+S△ABC,
∴![]() ABPE=
ABPE=![]() ACPF+
ACPF+![]() ABCH,
ABCH,
又∵AB=AC,
∴PE=PF+CH,
∴PE=7+3=10;
故答案为10或4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题
为发展校园足球运动,某区四校决定联合购买![]() 套队服和
套队服和![]() (
(![]() 且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多
且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多![]() 元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过
元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过![]() 套,则购买足球打八折
套,则购买足球打八折
(1)求每套队服和每个足球的价格是多少?
(2)请用含![]() 的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
(3)求出到甲、乙两家购买所需花的费用相同时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下表从左到右在毎个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2017个格子中的数字是( )
3 |
|
|
| -1 | 2 | …… |
A.3B.2C.0D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
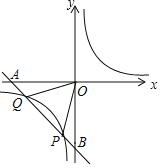
【题目】如图,已知反比例函数y=![]() (m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).
(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).
(1)求反比例函数与一次函数的表达式;
(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P点,连结OP、OQ,求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=![]() x与抛物线交于A、B两点,直线l为y=﹣1.
x与抛物线交于A、B两点,直线l为y=﹣1.
(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
(应用)请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
(拓展)计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com