
分析 (1)观察数字规律可知,结果为一个完全平方数,其底数为1+2+3+4+5;
(2)观察数字规律可知,结果为一个完全平方数,其底数为1+2+3+…+100;
(3)从1开始,连续n个正整数的立方和,等于这n个正整数和的平方.
解答 解:(1)依题意,得13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)依题意,得13+23+33+…+1003=(1+2+3+…+100)2=[$\frac{100(1+100)}{2}$]2=50502;
(3)一般规律为:13+23+33+…+n3=(1+2+3+…+n)2=[$\frac{n(1+n)}{2}$]2.
故答案为225;50502;[$\frac{n(1+n)}{2}$]2.
点评 本题是对数字变化规律的考查,观察出从1开始的连续正整数的立方和等于这些数的和的平方是解题的关键.


科目:初中数学 来源: 题型:填空题
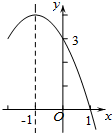 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5x-1 | B. | 5x+1 | C. | 13x-l | D. | 6x2+13x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com