
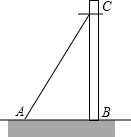
 如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | 无答案 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
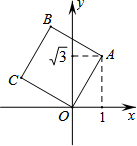 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
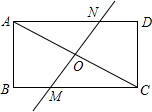 如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8
如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8查看答案和解析>>
科目:初中数学 来源: 题型:填空题
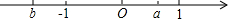 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
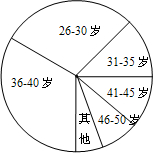 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
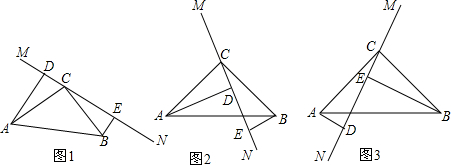
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com