
分析 根据题意所述可得出,若级数为N,天数为M,则M=N(N+4),然后3个月亮2个星星,和1个太阳1个月亮的天数即可得出结论.
解答 解:1级需要5天,2级需要12天;3级需要21天;四级需要32天…
∴若级数为N,天数为M,则M=N(N+4),
所以升到1个太阳1个月亮即到20级,则天数M=20(20+4)=480(天);
升到3个月亮2个星星即到第14级,所用天数为:14(14+4)=252(天),
所以480-252=228(天).即至少还需要228天.
故答案是:228.
点评 此题属于应用类问题,解答本题需要一定的规律总结能力,例如本题的规律“M=N(N+4)”,如果不能直接发现,可先计算出前几个级数、天数,然后再总结,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
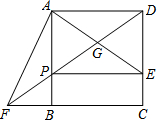 在正方形ABCD中,E是CD上一点,AF⊥AE交CB的延长线于点F,连接DF,分别交AE、AB于点G、P.已知∠BAF=∠BFD.
在正方形ABCD中,E是CD上一点,AF⊥AE交CB的延长线于点F,连接DF,分别交AE、AB于点G、P.已知∠BAF=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
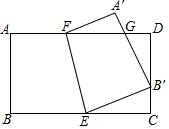 如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.
如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
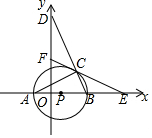 如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(-1,0)C(3,2$\sqrt{2}$),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(-1,0)C(3,2$\sqrt{2}$),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
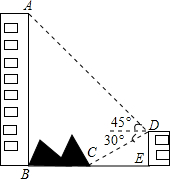 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com