
【题目】对于代数式![]() ,下列说法正确的是( )
,下列说法正确的是( )
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则![]() ;
;
②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c;
③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c;
④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c.
A.①B.③C.②④D.①③
【答案】B
【解析】
设y=ax2+bx+c(a≠0),根据二次函数的性质,二次函数与x轴的交点问题中根的判别式一一判断即可.
解:设y=ax2+bx+c(a≠0),
①当x=p或q时,ap2+bp+c与aq2+bq+c不一定等于0,故错误;
②根据二次函数的对称性,最多存在两个实数m≠n,使得am2+bm+c=an2+bn+c,故错误;
③∵ac<0,∴![]() =b2-4ac>0,∴抛物线与x轴有两个不同的交点,∴一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c,故正确;
=b2-4ac>0,∴抛物线与x轴有两个不同的交点,∴一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c,故正确;
④∵ac>0,∴![]() =b2-4ac不一定大于0,∴抛物线可能与x轴没有交点,∴不一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c,故错误.
=b2-4ac不一定大于0,∴抛物线可能与x轴没有交点,∴不一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c,故错误.
故答案为:B.


科目:初中数学 来源: 题型:
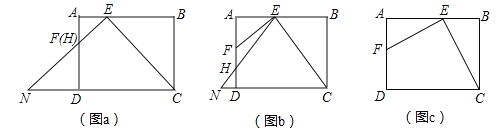
【题目】在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图a,当点H与点F重合时,求BE的长;
(2)如图b,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出它的定义域;
(3)连接AC,当△FHE与△AEC相似时,求线段DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
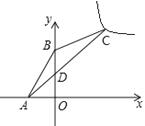
【题目】如图,在平面直角坐标系![]() 中,点A(
中,点A(![]() ,0),B(0,2),点C在第一象限,∠ABC=135°,AC交
,0),B(0,2),点C在第一象限,∠ABC=135°,AC交![]() 轴于D,CD=3AD,反比例函数
轴于D,CD=3AD,反比例函数![]() 的图象经过点C,则
的图象经过点C,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若房价定为200元时,求宾馆每天的利润;
(2)房价定为多少时,宾馆每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
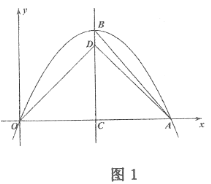
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,对称轴分别交抛物线和
,对称轴分别交抛物线和![]() 轴于点
轴于点![]() 和点
和点![]() ,以
,以![]() 为底边向上作等腰
为底边向上作等腰![]() .
.
(1)![]() ______;
______;![]() ______(用含
______(用含![]() 的代数式表示);
的代数式表示);
(2)如图1,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值;
的值;
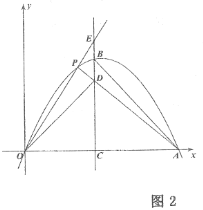
(3)点![]() 是抛物线
是抛物线![]() 段上任意一点,连接
段上任意一点,连接![]() 和
和![]() ,延长
,延长![]() 交对称轴于点
交对称轴于点![]() ,如图2,若
,如图2,若![]() ,
,![]() ,
,![]() 三点在一条直线上,当
三点在一条直线上,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
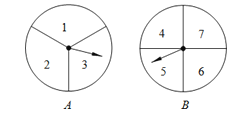
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月26日11:30,全球新冠肺炎确诊病例突破47万例,已有60个国家宣布进入紧急状态,国外较多医护人员不得不重复使用一次性口罩和防护装备.深圳海王星辰福田某药店购进A、B两种一次性口罩共1500个,已知购进A种一次性口罩和B种一次性口罩的费用分别为3000元和2000元,且A种一次性口罩的单价比B种一次性口罩单价多1元,求A、B两种一次性口罩的单价各是多少?设A种一次性口罩单价为x元,根据题意,列方程正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.抛物线开口向上B.抛物线与![]() 轴的交点在
轴的交点在![]() 轴负半轴上
轴负半轴上
C.当![]() 时,
时,![]() D.方程
D.方程![]() 的正根在3与4之间
的正根在3与4之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com