
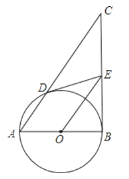
【题目】已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DFDC?若存在,作出点F,并予以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,理由见解析.
【解析】
(1)连接BD,已知ED、EB都是⊙O的切线,由切线长定理可证得OE垂直平分BD,而BD⊥AC(圆周角定理),则OE∥AC;由于O是AB的中点,可证得OE是△ABC的中位线,即E是BC中点,那么Rt△BDC中,DE就是斜边BC的中线,由此可证得所求的结论;(2)由(1)知:BC=2BE=2DE,则所求的比例关系式可转化为(![]() )2=DFDC,即DE2=DFDC,那么只需作出与△DEC相似的△DFE即可,这两个三角形的公共角为∠CDE,只需作出∠DEF=∠C即可;①∠DEC>∠C,即180°-2∠C>∠C,0°<∠C<60°时,∠DEF的EF边与线段CD相交,那么交点即为所求的F点;②∠DEC=∠C,即180°-2∠C=∠C,∠C=60°时,F与C点重合,F点仍在线段CD上,此种情况也成立;③∠DEC<∠C,即180°-2∠C<∠C,60°<∠C<90°时,∠DEF的EF边与线段的延长线相交,与线段CD没有交点,所以在这种情况下不存在符合条件的F点.
)2=DFDC,即DE2=DFDC,那么只需作出与△DEC相似的△DFE即可,这两个三角形的公共角为∠CDE,只需作出∠DEF=∠C即可;①∠DEC>∠C,即180°-2∠C>∠C,0°<∠C<60°时,∠DEF的EF边与线段CD相交,那么交点即为所求的F点;②∠DEC=∠C,即180°-2∠C=∠C,∠C=60°时,F与C点重合,F点仍在线段CD上,此种情况也成立;③∠DEC<∠C,即180°-2∠C<∠C,60°<∠C<90°时,∠DEF的EF边与线段的延长线相交,与线段CD没有交点,所以在这种情况下不存在符合条件的F点.
(1)证明:连接BD.
由于ED、EB是⊙O的切线,由切线长定理,得
ED=EB,∠DEO=∠BEO,
∴OE垂直平分BD.
又∵AB是⊙O的直径,
∴AD⊥BD.
∴AD∥OE.
即OE∥AC.
又O为AB的中点,
∴OE为△ABC的中位线,
∴BE=EC,
∴EB=EC=ED.
(2)解:在△DEC中,由于ED=EC,
∴∠C=∠CDE,
∴∠DEC=180°﹣2∠C.
①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F
满足条件.
在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求.
这是因为:
在△DCE和△DEF中,∵∠CDE=∠EDF,∠C=∠DEF,
∴△DEF∽△DCE.
∴DE2=DFDC.即(![]() BC)2=DFDC
BC)2=DFDC
∴BC2=4DFDC.
②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°,
此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DFDC.
③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点F在DC的延长线上,故线段DC上不存在满足条件的点F.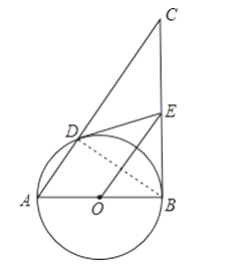


科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
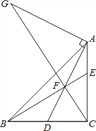
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.
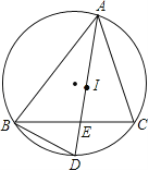
(1)求证:BD=ID;
(2)求证:ID2=DEDA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象上有一点P(m,n),其中坐标是关于t的一元二次方程t2﹣3t+k=0的两根,且P点到原点的距离为
的图象上有一点P(m,n),其中坐标是关于t的一元二次方程t2﹣3t+k=0的两根,且P点到原点的距离为![]() ,求反比例函数的解析式.
,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人轮流在黑板上写下不超过 ![]() 的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字( )时有必胜的策略.
A. 10 B. 9 C. 8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com