
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
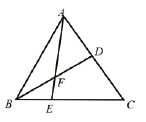
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为![]() 且
且![]() =24,则
=24,则![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元. 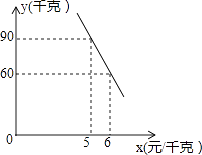
(1)根据题意,填写如表:
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为米(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过点A(﹣3,0),F(8,0),B(0,4)三点
(1)求抛物线解析式及对称轴;
(2)若点D在线段FB上运动(不与F,B重合),过点D作DC⊥轴于点C(x,0),将△FCD沿CD向左翻折,点B对应点为点E,△CDE与△FBO重叠部分面积为S.
①试求出S与x之间的函数关系式,并写出自变量取值范围.
②是否存在这样的点C,使得△BDE为直角三角形,若存在,求出C点坐标,若不存在,请说明理由;
(3)抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com