
 如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:
如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:分析 (1)根据观察函数图象的横坐标,可得早出发时间,晚到时间;
(2)根据函数图象的横坐标,可得相遇时间;
(3)根据待定系数法求函数解析式,可得答案.
解答 解:(1)由横坐标看出,骑自行车者比骑摩托车者早出发2小时,晚到2小时;
(2)由横坐标看出,骑摩托车者出发1小时后与骑自行车者在途中相遇;
故答案为:2,2,1;
(3)设自行车的函数解析式为y1=k1x ①,设摩托车的函数解析式为y2=k2x+b ②,
将(6,60)代入①,得6k1=60.
解得k1=10,
自行车的函数解析式为y1=10x;
将(2,0),(3,30)代入②得
$\left\{\begin{array}{l}{2{k}_{2}+b=0}\\{3{k}_{2}+b=30}\end{array}\right.$.
解得$\left\{\begin{array}{l}{{k}_{2}=30}\\{b=60}\end{array}\right.$.
故摩托车的函数解析式为y2=30x+60.
点评 本题考查了一次函数的应用,观察函数图象是解题关键,又利用了待定系数法求函数解析式.


科目:初中数学 来源: 题型:解答题
 已知:如图,AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为$\widehat{BF}$的中点.
已知:如图,AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为$\widehat{BF}$的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=3,AD=4,将此矩形折叠,使点D落在AB边上的点E处,折痕为FH,点C落在点Q处,EQ与BC交点G.设AE=x,四边形EFHQ的面积为y,则y关于x的函数解析式是y=$\frac{3}{8}$x2-$\frac{9}{8}$x+6..
如图,在矩形ABCD中,AB=3,AD=4,将此矩形折叠,使点D落在AB边上的点E处,折痕为FH,点C落在点Q处,EQ与BC交点G.设AE=x,四边形EFHQ的面积为y,则y关于x的函数解析式是y=$\frac{3}{8}$x2-$\frac{9}{8}$x+6..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
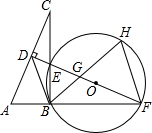 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com