
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.分析 (1)由横、竖彩条的宽度比为3:2知横彩条的宽度为$\frac{3}{2}$xcm,根据:三条彩条面积=横彩条面积+2条竖彩条面积-横竖彩条重叠矩形的面积,可列函数关系式;
(2)根据:三条彩条所占面积是图案面积的$\frac{2}{5}$,可列出关于x的一元二次方程,整理后求解可得.
解答 解:(1)根据题意可知,横彩条的宽度为$\frac{3}{2}$xcm,
∴$\left\{\begin{array}{l}{x>0}\\{20-2x>0}\\{12-\frac{3}{2}x>0}\end{array}\right.$,
解得:0<x<8,
y=20×$\frac{3}{2}$x+2×12•x-2×$\frac{3}{2}$x•x=-3x2+54x,
即y与x之间的函数关系式为y=-3x2+54x(0<x<8);
(2)根据题意,得:-3x2+54x=$\frac{2}{5}$×20×12,
整理,得:x2-18x+32=0,
解得:x1=2,x2=16(舍),
∴$\frac{3}{2}$x=3,
答:横彩条的宽度为3cm,竖彩条的宽度为2cm.
点评 本题主要考查根据实际问题列函数关系式及一元二次方程的实际应用能力,数形结合根据“三条彩条面积=横彩条面积+2条竖彩条面积-横竖彩条重叠矩形的面积”列出函数关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
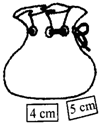 如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:
如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.
如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)-2=4 | B. | $\sqrt{{{(-2)}^2}}=-2$ | C. | 46÷(-2)6=64 | D. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠B=120°,∠D=50°,将∠C向内折出一个△PRC′,恰好使C′P∥AB,C′R∥AD,则∠C的度数是( )
如图,在四边形ABCD中,∠B=120°,∠D=50°,将∠C向内折出一个△PRC′,恰好使C′P∥AB,C′R∥AD,则∠C的度数是( )| A. | 80° | B. | 85° | C. | 95° | D. | 110° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com