
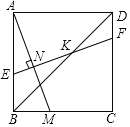
【题目】如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为______(用含x的代数式表示);
(2)设EK=2KF,则![]() 的值为______.
的值为______.
【答案】![]() x
x
【解析】
(1)根据勾股定理求得AM,进而得出AN,证得△AEN∽△AMB,由相似三角形的性质即可求得AE的长;
(2)连接AK、MG、CK,构建全等三角形和直角三角形,证明AK=MK=CK,再根据四边形的内角和定理得∠AKM=90°,利用直角三角形斜边上的中线等于斜边的一半得NK=![]() AM=AN,然后根据相似三角形的性质求得
AM=AN,然后根据相似三角形的性质求得![]() =
=![]() =x,即可得出
=x,即可得出![]() =x.
=x.
(1)解:∵正方形ABCD的边长为1,BM=x,
∴AM=![]() ,
,
∵点N是AM的中点,
∴AN=![]() ,
,
∵EF⊥AM,
∴∠ANE=90°,
∴∠ANE=∠ABM=90°,
∵∠EAN=∠MAB,
∴△AEN∽△AMB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AE=![]() ,
,
故答案为:![]() ;
;
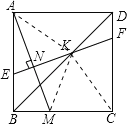
(2)解:如图,连接AK、MG、CK,
由正方形的轴对称性△ABK≌△CBK,
∴AK=CK,∠KAB=∠KCB,
∵EF⊥AM,N为AM中点,
∴AK=MK,
∴MK=CK,∠KMC=∠KCM,
∴∠KAB=∠KMC,
∵∠KMB+∠KMC=180°,
∴∠KMB+∠KAB=180°,
又∵四边形ABMK的内角和为360°,∠ABM=90°,
∴∠AKM=90°,
在Rt△AKM中,AM为斜边,N为AM的中点,
∴KN=![]() AM=AN,
AM=AN,
∴![]() =
=![]() ,
,
∵△AEN∽△AMB,
∴![]() =
=![]() =x,
=x,
∴![]() =x,
=x,
故答案为:x.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:EF=DH;
(2)若AB=6,DH=2DF,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出旋转后的点关于原点的对称点,这称为一次变换,已知点A的坐标为(﹣1,0),则点A经过连续2018次这样的变换得到的点A2018的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).
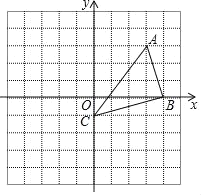
(1)以点C为中心,把△ABC逆时针旋转90°,请在图中画出旋转后的图形△A′B′C,点B′的坐标为________;
(2)在(1)的条件下,求出点A经过的路径![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
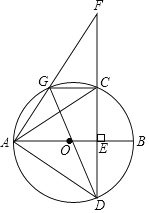
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
(1)求证:∠FGC=∠AGD;
(2)若AD=6.
①当AC⊥DG,CG=2时,求sin∠ADG;
②当四边形ADCG面积最大时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
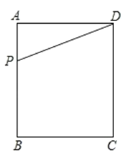
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一动点,连结
上的一动点,连结![]() .
.
(1)若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在矩形的对角线上点
落在矩形的对角线上点![]() 处,试求
处,试求![]() 的长;
的长;
(2)点![]() 运动到某一时刻,过点
运动到某一时刻,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,将
,将![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 折叠,点
折叠,点![]() 与点
与点![]() 分别落在点
分别落在点![]() ,
,![]() 处,若
处,若![]() ,
,![]() ,
,![]() 三点恰好在同一直线上,且
三点恰好在同一直线上,且![]() 试求此时
试求此时![]() 的长;
的长;
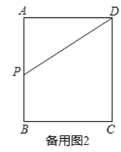
(3)当点![]() 运动到边
运动到边![]() 的中点处时,过点
的中点处时,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,将
,将![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合于点
重合于点![]() 处,连结
处,连结![]() ,请求出
,请求出![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com