
 某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
某城区规划局为了方便居民的生活,计划在三个住宅小区A,B,C(如图所示) 之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?分析 (1)根据线段垂直平分线上的点到线段两端点的距离相等,连接BC、AC,△ABC两边垂直平分线的交点就是花园的位置;
(2)利用垂直平分线的性质证明即可.
解答 (1)解:连接AB,分别以A、B为圆心,大于$\frac{1}{2}$AB为半径画弧,两弧交于两点,连接这两点即是作AB的垂直平分线;
同理连接BC,作出BC的垂直平分线,两条直线交于点P,则点P就是商场的位置;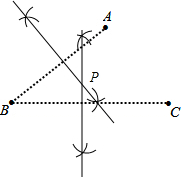
(2)证明:如图,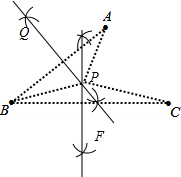
连接PA、PB、PC,
∵PF、PQ是BC、AB的垂直平分线,
∴PB=PC,PB=PA,
∴PA=PB=PC.
点评 此题主要考查了应用设计与作图,利用线段垂直平分线上的点到线段两端点的距离相等的性质解决问题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x2-3 | B. | y=x2+2x | C. | y=-$\frac{1}{3}$(x-1)2-1 | D. | y=-$\frac{1}{3}$x2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com