
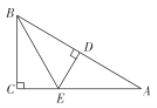
【题目】如图,在![]() ,
,![]() ,
,![]() ,作
,作![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.2B.1C.![]() D.3
D.3
科目:初中数学 来源: 题型:
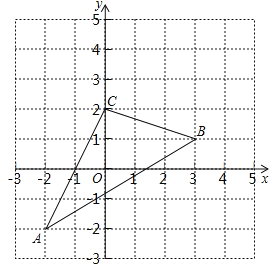
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
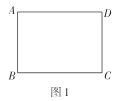
综合与实践课上,老师让同学们以“折纸”为主题开展数学活动.如图1,有一张长为4,宽为3的矩形纸片![]() (
(![]() ).
).
操作发现
(1)快乐小组先将图1中的矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在点
落在点![]() 处,得到图2,他们发现
处,得到图2,他们发现![]() ,请你证明这个结论;
,请你证明这个结论;
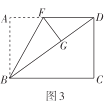
(2)创新小组将图2中的矩形纸片展开后继续折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,得到图3,则折痕
,得到图3,则折痕![]() __________;
__________;
实践探究
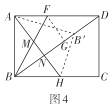
(3)前进小组在创新小组的操作基础上,将图3中的纸片展开,再将矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
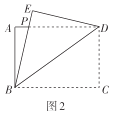
上的点![]() 处,然后将纸片展平.如图4所示,折痕
处,然后将纸片展平.如图4所示,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=![]() x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
(1)求该抛物线的函数表达式及顶点D的坐标;
(2)判断△ABC的形状,并求出△ABC的面积;
(3)将抛物线向左或向右平移,得到抛物线L′,L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com