

���� ��1���������A��B���꣬�ٽ�����������C�����꣬���������߽���ʽ�����a��ֵ��
��2���������D�����꣬��E��ET��y���ڵ�T�������E�����꣬���ô���ϵ���������ֱ��BE�Ľ���ʽ���Ӷ�����õ�F�����꣬������DF������t��ʾ��S��
��3���������������E��D��F�����꣬�����ֱ��DE�Ľ���ʽ����DE��x���ڵ�K������KF����EM��y���ڵ�H��GM��EM�ڵ�M��EN��y���ڵ�N�������K�����꣬���������֤����FOK�ա�EHF���Ӷ�����á�FEK=��FKE=45�㣬�ɵõ���GEM=��DEN�������ýǵ�����ֵ�ɵõ�$\frac{GM}{EM}$=$\frac{DN}{EN}$�����G�����꣬�ɱ�ʾ��GM��EM����������G�����꣮
��� �⣺
��1����y=0ʱ������a��x+3����x-4��=0��
���x=-3��x=4��
��A��-3��0����B��4��0����
��AB=7����AB-OC=1��
��OC=6��
��C��0��6����
���������߽���ʽ�ɵ�-12a=6�����a=-$\frac{1}{2}$��
��2����ͼ1����E��ET��y���ڵ�T��
��B��4��0����
��OB=4��
��BD=5��
��OD=3��
��D��0��-3����
��a=-$\frac{1}{2}$��
�������߽���ʽΪy=-$\frac{1}{2}$��x+3����x-4����
��E�������Ϊt������������Ϊ-$\frac{1}{2}$��t+3����t-4����
��ֱ��BE����ʽΪy=kx+b����B��E�������ɵ�$\left\{\begin{array}{l}{kt+b=-\frac{1}{2}��t+3����t-4��}\\{4k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}��t+3��}\\{b=2��t+3��}\end{array}\right.$��
��ֱ��BE�Ľ���ʽΪy=-$\frac{1}{2}$��t+3��x+2��t+3����
��x=0�ɵ�y=2��t+3����
��F��0��2t+6����
��DF=2t+6-��-3��=2t+9��
��S=$\frac{1}{2}$��2t+9����4-t��=-t2-$\frac{1}{2}$t+18��
��E���ڵڶ����ޣ�
��t��ȡֵ��ΧΪ-3��t��0��
��3����-t2-$\frac{1}{2}$t+18=15�ɽ��t=$\frac{3}{2}$����ȥ����t=-2��
��E��-2��3����F��0��2����
��ֱ��DE�Ľ���ʽΪy=sx+t����D��E�������ɵ�$\left\{\begin{array}{l}{-2t+s=3}\\{s=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{t=-3}\\{s=-3}\end{array}\right.$��
��ֱ��DE�Ľ���ʽΪy=-3x-3��
��ͼ2����DE��x���ڵ�K������KF����EM��y���ڵ�H��GM��EM�ڵ�M��EN��y���ڵ�N��
��K��-1��0����
��EH=2=OF��HF=OK=1���ҡ�FOK=��EHF=90�㣬
�ڡ�FOK�͡�EHF��
$\left\{\begin{array}{l}{OF=EH}\\{��FOK=��EHF}\\{OK=HF}\end{array}\right.$
���FOK�ա�EHF��SAS����
��EF=KF����EFH=��FKO��
�ߡ�FKO+��KFO=��EFH+��KFO=90�㣬
���EFK=90�㣬
���FEK=��FKE=45�㣬
���GED=90�㣬
�ߡ�MEN=90�㣬
���GEM+��MED=��DEN+��MED��
���GEM=��DEN��
��tan��GEM=tan��DEN��
��$\frac{GM}{EM}$=$\frac{DN}{EN}$��
��G��������m��-$\frac{1}{2}$m2+$\frac{1}{2}$m+6����
��M��m��3����N��-2��-3����
��GM=-$\frac{1}{2}$m2+$\frac{1}{2}$m+6-3=-$\frac{1}{2}$m2+$\frac{1}{2}$m+3��EM=m+2��DN=2��EN=6��
��$\frac{-\frac{1}{2}{m}^{2}+\frac{1}{2}m+3}{m+2}$=$\frac{2}{6}$�����m=-2����ȥ����m=$\frac{7}{3}$��
��G��������$\frac{7}{3}$��$\frac{40}{9}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ���������ɶ���������ͼ����������Ľ��㡢ȫ�������ε��ж������ʡ����Ǻ����Ķ���ȣ��ڣ�1�������C�������ǽ���Ĺؼ����ڣ�2������t��ʾ��F��������ǽ���Ĺؼ����ڣ�3����֤�á�GEM=��DEN�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������OAB����һ����P��P�ӵ�A��������$\widehat{AB}$���߶�BO���߶�OA�����˶�����A����OP�ij���y���˶�ʱ��t֮��ĺ���ͼ������� ��������
��ͼ������OAB����һ����P��P�ӵ�A��������$\widehat{AB}$���߶�BO���߶�OA�����˶�����A����OP�ij���y���˶�ʱ��t֮��ĺ���ͼ������� ��������| A�� |  | B�� |  | C�� | 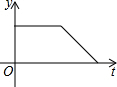 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� ��� | ƽʱ���� | ���� ���� | ��ĩ ���� | |||
| ��1�� | ��2�� | ��3�� | ��4�� | |||
| �ɼ� | 80 | 86 | 84 | 90 | 90 | 95 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊy1�������صľ���Ϊy2���ͳ���ʻʱ��Ϊx����y1��y2��x�ĺ�����ϵͼ����ͼ��ʾ����������˵����
һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊy1�������صľ���Ϊy2���ͳ���ʻʱ��Ϊx����y1��y2��x�ĺ�����ϵͼ����ͼ��ʾ����������˵����| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com