
等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕点P旋转.
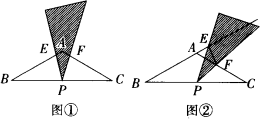
(1)如图①,当三角板的两边分别交AB,AC于点E,F时.求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图②情形时,三角板的两边分别交BA的延长线于点E,交边AC于点F.
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由.
|
(1)∵AB=AC=8,∠BAC=120°,∴∠B=∠C=30°,∴∠BPE+∠BEP=150°,∵∠EPF=30°,∴∠BPE+∠FPC=150°,∴∠BEP=∠CPF,∴△BPE∽△CFP. (2)①探究1:△BPE与△CFP相似,其理由与第(1)小题相同.②探究2:∵△BPE∽△CFP,∴BE∶PC=PE∶PF,∵P为BC的中点,∴PB=PC,∴BE∶PB=PE∶PF,∵∠EPF=∠B=30°,∴△BPE∽△PFE. |
|
判定两个三角形相似有三种方法:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;如果两个三角形的两组对应边的比相等,并且夹角相等,那么这两个三角形相似;如果两个三角形的三组对应边的比相等,那么这两个三角形相似. |


科目:初中数学 来源: 题型:022
查看答案和解析>>
科目:初中数学 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:013
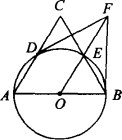
如图等腰△ABC,AB=AC,以AB为直径作⊙O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连结FD,下列结论:①![]() ;②FD是⊙O的切线;③∠C=∠DFB;④AD·OF=2OA2.其中一定正确的结论是
;②FD是⊙O的切线;③∠C=∠DFB;④AD·OF=2OA2.其中一定正确的结论是
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源:浙江省长兴县2012届九年级上学期期中考试数学试题 题型:044
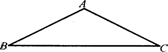
已知等腰△ABC,AB=AC=4,∠BAC=1200,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
查看答案和解析>>
科目:初中数学 来源:北京市怀柔区2011年中考一模数学试题 题型:044
等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小亮拿着30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
(1)如图,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
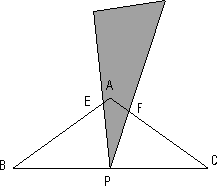
(2)操作:将三角板绕点P旋转到下图情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
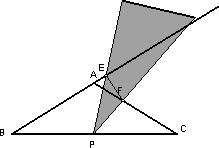
①探究1:△BPE与△CFP还相似吗?
②探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
设EF=m,△EPF的面积为S,试用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源:2013年江西省南昌市高级中等学校招生考试数学 题型:044
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
(1)操作发现:
在等腰△ABC,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是________(填序号即可)

①AF=AG=![]() AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME
AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME
(2)数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系?请给出证明过程;

(3)类比探究:
(i)在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,试判断△MEC的形状.答:________.

(ii)在三边互不相等的△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作(非等腰)直角三角形ABD和(非等腰)直角三角形ACE,M是BC的中点,连接MD和ME,要使(2)中的结论时仍然成立,你认为需增加一个什么样的条件?(限制用题中字母表示)并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com