
 学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?
学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?  暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为$\frac{2-\sqrt{2}}{4}$.
如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为$\frac{2-\sqrt{2}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
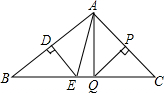 如图,在△ABC中,AB的垂直平分线交BC于E,垂足为D,AC的垂直平分线交BC于Q,垂足为P.
如图,在△ABC中,AB的垂直平分线交BC于E,垂足为D,AC的垂直平分线交BC于Q,垂足为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
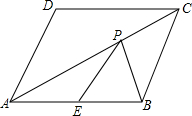 已知,菱形ABCD中,∠ADC=120°,AD=6,E是AB的中点,P是对角线AC上一点,求PE+PB的最小值,并在AC上找出此时点P的位置(保留作图痕迹)
已知,菱形ABCD中,∠ADC=120°,AD=6,E是AB的中点,P是对角线AC上一点,求PE+PB的最小值,并在AC上找出此时点P的位置(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为$\sqrt{2}$的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是$\frac{2}{3}$.
如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为$\sqrt{2}$的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com