
点A(-1,0)B(4,0)C(0,2)是平面直角坐标系上的三点。
① 如图10-1先过A、B、C作△ABC,然后在在 轴上方作一个正方形D1E1F1G1,
轴上方作一个正方形D1E1F1G1,
使D1E1在AB上, F1、G1分别在BC、AC上
② 如图10-2先过A、B、C作圆⊙M,然后在 轴上方作一个正方形D2E2F2G2,
轴上方作一个正方形D2E2F2G2,
使D2E2在 轴上 ,F2、G2在圆上
轴上 ,F2、G2在圆上
③ 如图10-3先过A、B、C作抛物线 ,然后在
,然后在 轴上方作一个正方形D3E3F3G3,
轴上方作一个正方形D3E3F3G3,
使D3E3在 轴上, F3、G3在抛物线上
轴上, F3、G3在抛物线上
(1)请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小
(2)并简要小结解决此题所用的方法或定理。

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
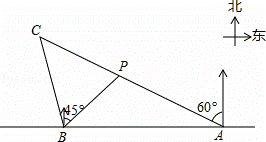
如图,在一笔直的海岸线上有A、B两个观测站,A在B的正东方向,AB=2(单位km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y= a(x﹣1)2+c与x轴交于点A(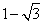 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道,代数式包括整式、分式以及根式。
(1)请你写出一个只含有字母 的二次三项式,并且不论当
的二次三项式,并且不论当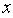 为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。
为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。
(2)请你写出一个只含有字母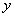 的代数式,并且使代数式有意义的
的代数式,并且使代数式有意义的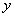 的取值范围为
的取值范围为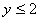 且
且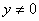 。请你写出的代数式。
。请你写出的代数式。
查看答案和解析>>
科目:初中数学 来源: 题型:
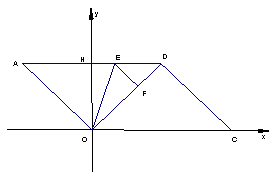
如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与y轴交与点H,CD=10,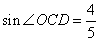 。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),
。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),
∠OEF=∠A=∠DOC,设AE=t,OF=s。
(1) 求直线DC的解析式;
(2) 求s关于t的函数关系式,并写出t的取值范围;
(3) 点E在边AD上移动的过程中,△OEF是否有可能成为一个等腰三角形?若有可能,请求出t的值,若不可能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com