
 如图所示,在一次“寻宝”游戏中,已知寻宝图上两个标志点A(-3,0)和点B(5,0),宝藏分别埋在C(3,4)和D(-2,3)两点.请你首先建立直角坐标系确定宝藏的位置,然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积.
如图所示,在一次“寻宝”游戏中,已知寻宝图上两个标志点A(-3,0)和点B(5,0),宝藏分别埋在C(3,4)和D(-2,3)两点.请你首先建立直角坐标系确定宝藏的位置,然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积. 科目:初中数学 来源: 题型:解答题
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
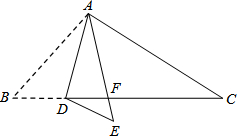 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com