
���� ��1���������ʽ�Ķ��弴���жϣ�
��2����������ѷ�ʽ�ķ��ӻ���x+2����ʽ��Ȼ������ͬ��ĸ�ķ�ʽ�ļӷ�������⣻
��3����ʽ$\frac{2x-1}{x+1}$��Ϊ����ʽ���ѷ��ӻ���2��x+1��-3����ʽ��Ȼ������ͬ��ĸ�ķ�ʽ�ļӷ����ɴ���ʽ��
$\frac{2x-1}{x+1}$��ֵΪ��������$\frac{3}{x+1}$��ֵһ������������x+1һ����3��Լ�����Ӷ����x��ֵ��
��� �⣺��1��$\frac{2}{x}$�����ʽ���ʴ��ǣ��棻
��2��$\frac{x-1}{x+2}$=$\frac{x+2-3}{x+2}$=1-$\frac{3}{x+2}$��
�ʴ��ǣ�1-$\frac{3}{x+2}$��
��3��$\frac{2x-1}{x+1}$=$\frac{2x+2-3}{x+1}$=$\frac{2��x+1��-3}{x+1}$=2-$\frac{3}{x+1}$��
��$\frac{2x-1}{x+1}$��ֵΪ��������xΪ������
��x+1Ϊ3��Լ����
��x+1��ֵΪ1��-1��3��-3��
��x��ֵΪ0��-2��2��-4��
���� ���⿼���˷�ʽ�Ļ�����㣬��ȷ�Է�ʽ�ķ�ĸ���б��Σ�����ͬ��ĸ�ķ�ʽ�ļӷ������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ��
��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
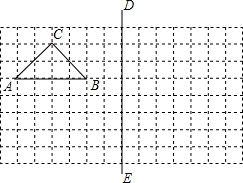 ��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺
��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=4��BC=6���Խ���AC��BD���ڵ�O���ӳ�DC��E������OE����BC�ڵ�F����CE=2������CF�ij���
��ͼ������ABCD�У�AB=4��BC=6���Խ���AC��BD���ڵ�O���ӳ�DC��E������OE����BC�ڵ�F����CE=2������CF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����x����������A��-3��0����B��3��0������һ����C���߶�AB�ϴӵ�A�˶�����B������A��B�غϣ����ֱ���AC��BCΪ�ױ���������AEC�͵�����BFC������E��Fǡ�����ڷ���������y=-$\frac{5}{x}$��x��0����y=$\frac{2}{x}$��x��0����ͼ���ϣ�����EF���������˶������У��߶�EF���ȵı仯����ǣ�������
��ͼ����x����������A��-3��0����B��3��0������һ����C���߶�AB�ϴӵ�A�˶�����B������A��B�غϣ����ֱ���AC��BCΪ�ױ���������AEC�͵�����BFC������E��Fǡ�����ڷ���������y=-$\frac{5}{x}$��x��0����y=$\frac{2}{x}$��x��0����ͼ���ϣ�����EF���������˶������У��߶�EF���ȵı仯����ǣ�������| A�� | һֱ���� | B�� | һֱ��С | C�� | ��������С | D�� | �ȼ�С������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
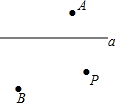 ��ͼ��ƽ������ֱ��a��ֱ��a�������A��B��P��
��ͼ��ƽ������ֱ��a��ֱ��a�������A��B��P���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com