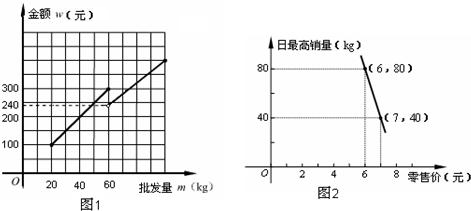
解:(1)当批发量≤60千克时,函数图象经过点(20,100)和(60,300)
设解析式为y=k
1x+b
1,
∴
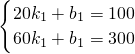
解得:
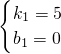
∴函数关系式为y=5x(20≤x≤60);
当批发量≥60千克时,函数图象经过点(60,240)和(100,400)
设解析式为y=k
2x+b
2,
∴
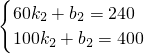
解得:
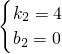
∴函数关系式为y=4x(60<x≤100);
(2)240÷60=4元/千克,
∴批发量超过60kg时,该种水果的批发价为4元/kg;
(3)设日最高销售量为xkg(x>60),日零售价为p,
则由图②日零售价p满足:x=320-40p,于是p=
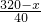
销售利润y=x(
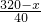
-4)=-

(x-80)
2+160
当x=80时,y
最大值=160,
此时p=6
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.
分析:(1)根据函数图象经过的点利用待定系数法求得函数的解析式即可;
(2)用240除以60即可得到水果的批发价;
(3)可根据图中给出的信息,用待定系数的方法来确定函数.然后根据函数的特点来判断所要求的值.
点评:此题主要考查了分段函数、一次函数、二次函数的性质和应用,难点在于分段函数不熟,同学们应注意有意识的训练分段函数中数形结合的应用.


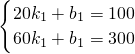
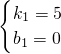
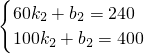
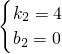
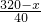
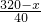 -4)=-
-4)=- (x-80)2+160
(x-80)2+160

 名校课堂系列答案
名校课堂系列答案