【题目】如图，已知直线
与
轴、
轴分别交于
，
两点，
是以
为圆心，1为半径的圆上一动点，连接
，
，当
的面积最大时，点的坐标为__________．
科目：初中数学 来源： 题型：
【题目】4件同型号的产品中，有1件不合格品和3件合格品．
（1）从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；
（2）从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
（3）在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在
中，
，
是的外接圆，过点
作
交于点
，连接
交
于点
，延长
至点
，使
，连接
.
（1）求证：
；
（2）求证：是的切线；
（3）如图2，若点
是
的内心，
，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的y与x的部分对应值如表：
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论：①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(
,2),B(
,3)是抛物线上两点,则
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
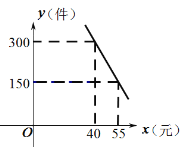
【题目】“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量
（件）与销售单价
（元）之间存在一次函数关系，如图所示.
（1）求与之间的函数关系式；
（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？
（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过
三点
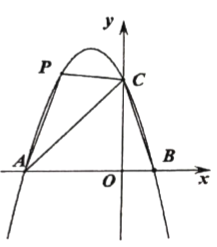
（1）求抛物线的解析式；
（2）在直线
上方的抛物线上是否存在一点
，使
的面积等于
的面积的一半？若存在，求出点的坐标；若不存在，说明理由；
（3）点
为抛物线上一动点，在
轴上是否存在点
，使以
，
，，为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，AB=2，AD=4，对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点，则下列说法正确的是（ ）
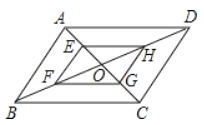
A.EH=HGB.四边形EFGH是平行四边形
C.AC⊥BDD.
的面积是
的面积的2倍
查看答案和解析>>
科目：初中数学 来源： 题型：
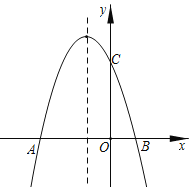
【题目】如图，已知抛物线y＝﹣x2+bx+3的对称轴为直线x＝﹣1，分别与x轴交于点A，B（A在B的左侧），与y轴交于点C．
（1）求b的值；
（2）若将线段BC绕点C顺时针旋转90°得到线段CD，问：点D在该抛物线上吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
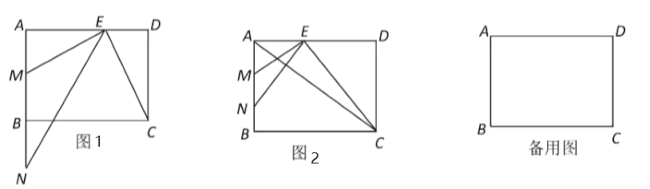
【题目】在矩形
中，
，
，点
是边
上一点，
交
于点
，点
在射线
上，且
是
和
的比例中项．
（1）如图1，求证：
；
（2）如图2，当点在线段之间，联结
，且与
互相垂直，求
的长；
（3）联结，如果
与以点、、为顶点所组成的三角形相似，求
的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
