
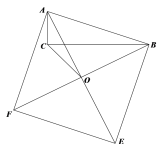
【题目】如图,以Rt![]() 的斜边AB为一边在
的斜边AB为一边在![]() 同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,
同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,![]() ,那么四边形ABOC的面积为_______.
,那么四边形ABOC的面积为_______.
【答案】![]()
【解析】
在BC上取一点D,使BD=AC=2,连接OD,可证得△BOD≌△AOC,得到OD=OC=![]() ,再得到△COD是等腰直角三角形,根据勾股定理求出CD,故得到BC的长,再求出△ABC,△BCO的面积即可.
,再得到△COD是等腰直角三角形,根据勾股定理求出CD,故得到BC的长,再求出△ABC,△BCO的面积即可.
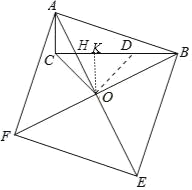
如图,在BC上取一点D,使BD=AC=2,连接OD,作OK⊥BC于K,
∵∠CAO=90°-∠AHC,∠OBD=90°-∠OHB,
∵∠AHC=∠OHB,
∴∠CAO=∠OBD
∵四边形ABEF是正方形,
∴OA=OB, BD=AC
∴△BOD≌△AOC,
OD=OC=![]() ,∠BOD=∠AOC,
,∠BOD=∠AOC,
∵∠BOD+∠DOH=90°,
∴∠DOH+∠COA=90°,即∠COD=90°,
∴△COD是等腰直角三角形,
∴CD=![]() ,OK=
,OK=![]()
∴BC=![]()
∴四边形ABOC的面积=![]() =
=![]() =
=![]()
故填:![]()


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
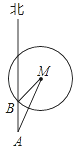
【题目】如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( )
A. (![]() ﹣1)小时 B. (
﹣1)小时 B. (![]() +1)小时 C. 2小时 D.
+1)小时 C. 2小时 D. ![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
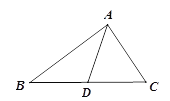
【题目】如图:在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( ).
A. 2<AD<8B. 0<AD<8C. 1<AD<4D. 3<AD<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在长方形的边上.
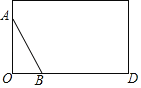
(1)用圆规和无刻度的直尺在长方形的内部作∠ABC=∠ABO;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若BE是∠CBD的角平分线,探索AB与BE的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂计划一周生产某种玩具700件,平均每天生产100件,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -6 | +6 | -3 |
(1)根据记录的数据可知该厂星期四生产玩具 件;
(2)产量最多的一天比产量最少的一天多生产玩具 件;
(3)根据记录的数据可知该厂本周实际生产玩具 件;
(4)该厂实行每周计件工资制,每生产一件玩具可得20元,若超额完成任务,则超过部分每件另奖5元;少生产一件扣4元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试根据图中信息,解答下列问题.

(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
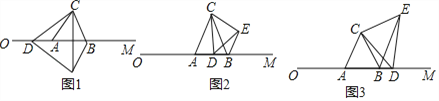
【题目】(14分)如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连结DE.
(1)求证:△CDE是等边三角形;
(2)如图2,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;
(3)如图3,当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是过点
是过点![]() 的一条射线,
的一条射线,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .请回答下列问题:
.请回答下列问题:
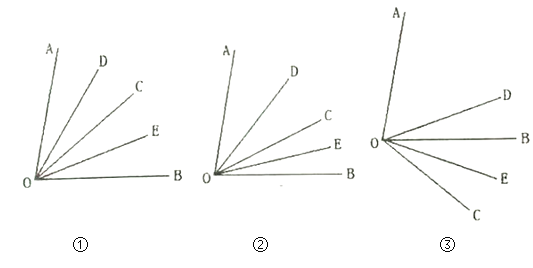
(1)如图①,如果![]() 是
是![]() 的平分线,求
的平分线,求![]() 的度数是多少?
的度数是多少?
(2)如图②,如果![]() 是
是![]() 内部的任意一条射线,
内部的任意一条射线,![]() 的度数有变化吗?为什么?
的度数有变化吗?为什么?
(3)如图③,如果![]() 是
是![]() 外部的任意一条射线,
外部的任意一条射线,![]() 的度数能求出吗?如果能求出,请写出过程;如果不能求出,请简要说明理由.
的度数能求出吗?如果能求出,请写出过程;如果不能求出,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y+1与x+2成正比例,且当x=4时,y=-4.
(1)求y关于x的函数关系式;
(2)若点(a,2)和(2,b)均在(1)中函数图像上,求a、b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com