
分析 (1)根据解一元一次不等式组的方法可以解答本题;
(2)①根据平方差公式可以分解因式,
②根据完全平方公式和平方差公式可以分解因式;
(3)先化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:(1)$\left\{\begin{array}{l}{3x+1>4}&{①}\\{4-2x≥0}&{②}\end{array}\right.$,
由不等式①,得
x>1,
由不等式②,得
x≤2,
故原不等式组的解集是1<x≤2;
(2)①(a+2b)2-(2a-b)2
=[(a+2b)+(2a-b)][(a+2b)-(2a-b)]
=(3a+b)(-a+3b);
②4-x2+2xy-y2
=4-(x2-2xy+y2)
=4-(x-y)2
=[2+(x-y)][2-(x-y)]
=(2+x-y)(2-x+y);
(3)$\frac{(2-x)(4-x)}{{x}^{2}-16}$÷($\frac{x-2}{4-3x}$)2•$\frac{{x}^{2}+2x-8}{(x-3)(3x-4)}$
=$\frac{(2-x)(4-x)}{(x+4)(x-4)}•\frac{(4-3x)^{2}}{(x-2)^{2}}$$•\frac{(x+4)(x-2)}{(x-3)(3x-4)}$
=$\frac{3x-4}{x-3}$,
当x=4时,原式=$\frac{3×4-4}{4-3}$=8.
点评 本题考查分式的化简求值、因式分解法、解一元一次不等式组,解答本题的关键是明确它们各自的计算方法.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
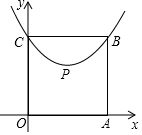 【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6
【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
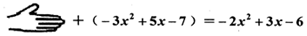
| x | 所捂的代数式的值 |
| 1 | 0 |
| 2 | 1 |
| 3 | 4 |
| 4 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形DABC的顶点D是原点,顶点B到y轴上,菱形的两条对角线分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为-6.
如图,菱形DABC的顶点D是原点,顶点B到y轴上,菱形的两条对角线分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com