
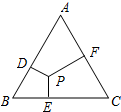
 如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )
如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 首先连接PA、PB、PC,再根据正三角形的面积的求法,求出边长为2的正三角形的面积是多少;然后判断出SABC=SAPB+SAPC+SBPC=PD+PE+PF,据此求出PD+PE+PF的值为多少即可.
解答 解:如图,连接PA、PB、PC,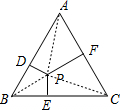 ,
,
∵△ABC是边长为2的正三角形,
∴△ABC的面积为:
$\frac{\sqrt{3}}{4}{×2}^{2}=\sqrt{3}$;
∵SABC=SAPB+SAPC+SBPC
=$\frac{1}{2}$×2×PD+$\frac{1}{2}$×2×PF+$\frac{1}{2}$×2×PE
=PD+PE+PF
∴PD+PE+PF=$\sqrt{3}$,
即PD+PE+PF的值为$\sqrt{3}$.
故选:B.
点评 (1)此题主要考查了等边三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等边三角形的三个内角都相等,且都等于60°.②等边三角形是轴对称图形,它有三条对称轴;③它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.
(2)此题还考查了等边三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:边长是a的等边三角形的面积是$\frac{\sqrt{3}}{4}$a2.


科目:初中数学 来源: 题型:选择题
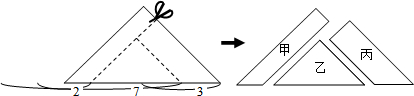
| A. | 乙>丙>甲 | B. | 丙>乙>甲 | C. | 甲>丙>乙 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
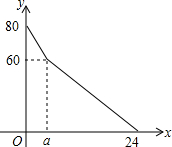 某超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待自助收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
某超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待自助收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
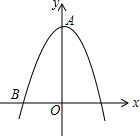 如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).
如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.6×105 | B. | 96×105 | C. | 9.6×106 | D. | 96×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 | 1 | 2 | 3 | 4 | 5 | 6 | 总和/h | 平均数/h |
| A厂家电池使用时间/h | 40 | 48 | 40 | 42 | 43 | 45 | ||
| B厂家电池使用时间/h | 40 | 50 | 45 | 46 | 46 | 52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com