


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
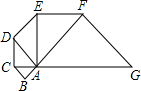 如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为
如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
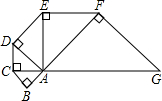 如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为
如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建晋江养正中学八年级上学期期中考试数学试题(带解析) 题型:解答题
如图,已知等腰直角三角形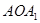 的直角边长为1,以Rt△
的直角边长为1,以Rt△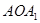 的斜边
的斜边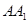 为直角边,画第二个等腰直角三角形
为直角边,画第二个等腰直角三角形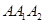 ,再以Rt△
,再以Rt△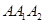 的斜边
的斜边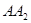 为直角边,画第三个等腰直角三角形
为直角边,画第三个等腰直角三角形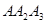 ,…,以此类推;
,…,以此类推;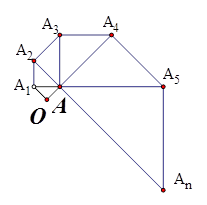
(1)第5个等腰直角三角形的斜边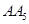 长是________________;
长是________________;
(2)第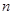 个等腰直角三角形的斜边
个等腰直角三角形的斜边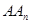 长是________________;(用含
长是________________;(用含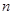 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建晋江养正中学八年级上学期期中考试数学试题(解析版) 题型:解答题
如图,已知等腰直角三角形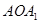 的直角边长为1,以Rt△
的直角边长为1,以Rt△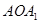 的斜边
的斜边 为直角边,画第二个等腰直角三角形
为直角边,画第二个等腰直角三角形 ,再以Rt△
,再以Rt△ 的斜边
的斜边 为直角边,画第三个等腰直角三角形
为直角边,画第三个等腰直角三角形 ,…,以此类推;
,…,以此类推;

(1)第5个等腰直角三角形的斜边 长是________________;
长是________________;
(2)第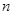 个等腰直角三角形的斜边
个等腰直角三角形的斜边 长是________________;(用含
长是________________;(用含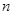 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(解析版) 题型:填空题
如图,已知等腰Rt△ABC的直角边长为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推直到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com