
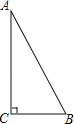
【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)动手操作:利用尺规作∠ABC的平分线,交AC于点O,再以O为圆心,OC的长为半径作⊙O(保留作图痕迹,不写作法);
(2)综合运用:在你所作的图中,
①判断AB与⊙O的位置关系,并证明你的结论;
②若AC=12,tanOBC=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)AB与⊙O相切,理由见解析;(3)![]()
【解析】试题分析:(1)只需按照题目的要求画图即可;
(2)①过点O作OD⊥AB,垂足为D,如图所示,只需证明OD=OC即可;②在Rt△OBC中,运用三角函数可求出![]() ,从而得到
,从而得到![]() ,易证Rt△ADO∽Rt△ACB,运用相似三角形的性质可求得AD=8,然后在Rt△ADO中运用勾股定理即可解决问题.
,易证Rt△ADO∽Rt△ACB,运用相似三角形的性质可求得AD=8,然后在Rt△ADO中运用勾股定理即可解决问题.
试题解析:(1)如图,⊙O即为所求作;

(2)AB与⊙O相切,理由如下:
过点O作OD⊥AB,垂足为D,如图所示.
∵∠ACB=90°,∴OC⊥BC.
∵BO是∠ABC的平分线,OD⊥AB,OC⊥BC,
∴OC=OD.
∴AB与⊙O相切;
(3)在Rt△OBC中,
tan∠OBC=![]()
∴![]() .
.
又∵∠ADO=∠ACB=90°,∠A=∠A,
∴Rt△ADO∽Rt△ACB,
∴![]() ,
,
∴AD=![]() AC=
AC=![]() ×12=8.
×12=8.
设⊙O的半径为r,则OD=OC=r,AO=12-r.
在Rt△ADO中,
根据勾股定理可得r2+82=(12-r)2,
解得r=![]() ,
,
∴⊙O的半径是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( )个
①垂线段最短 ②直线外一点到这条直线的垂线段叫做点到直线的距离
③过一点有且只有一条直线与已知直线平行
④不相交的两条直线互相平行
⑤垂直于同一直线的两条直线互相平行
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数轴上的A、B、C三点表示的实数分别为a、1、﹣1,则|a+1|表示( )
A.A、B两点间的距离
B.A、C两点间的距离
C.A、B两点到原点的距离之和
D.A、C两点到原点的距离之和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华要从长度分别为 5cm,6cm,11cm,16cm 的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒形成的三角形的周长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州市总投资为443亿元的轨道交通1、2、3号线同时共建中,建成后将有效缓解我市交通压力、便利市民出行、提高城市整体实力,443亿用科学记数法表示为( )
A.0.443×1010
B.4.43×109
C.443×108
D.4.43×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com