
���� ��1���ֱ�����Ͷ����112��Ԫ������40���������г�վ�㡢����720���������г��Լ�Ͷ��340.5��Ԫ���½�120���������г�վ�㡢����2205���������г������ó���ʽ����𰸣�
��2������2016������720���������г������������Ϊx��������ʾ��2018�����ù������г��������ó���ʽ����𰸣�
��� �⣺��1����ÿ��վ�����x��Ԫ�����г�����Ϊy��Ԫ����������ɵã�
$\left\{{\begin{array}{l}{40x+720y=112}\\{120x+2205y=340.5}\end{array}}\right.$
��ã�$\left\{{\begin{array}{l}{x=1}\\{y=0.1}\end{array}}\right.$
��ÿ��վ�����Ϊ1��Ԫ�����г�����Ϊ0.1��Ԫ��
��2����2016�굽2018�����������ù������г���������ƽ��������Ϊa��
��������ɵã�720��1+a��2=2205
��˷��̣���1+a��2=$\frac{49}{16}$��
����a1=$\frac{3}{4}$=75%��a2=-$\frac{11}{4}$�����������⣬��ȥ��
��2016�굽2018�����������ù������г���������ƽ��������Ϊ75%��
���� ������Ҫ�����˶�Ԫһ�η��̵�Ӧ���Լ�һԪ���η��̵�Ӧ�ã���ȷ�ó���ʽ�ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ʊ�н��ĸ�����1%������100�Ų�Ʊһ�����н� | |
| B�� | һ�����ݵ���λ�����������������м���� | |
| C�� | Ь���ϰ����ʱ����ĵ���Ь������� | |
| D�� | ��ÿ�ο��Գɼ������Һã���S��2��S��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2��0��y1 | B�� | y1��y2��0 | C�� | y1��0��y2 | D�� | y2��y1��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
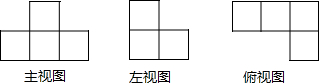
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
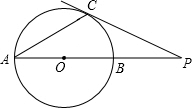 ��ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ�����C��������AB���ӳ��߽��ڵ�P������AC������A=30�㣬PC=3����BP�ij�Ϊ$\sqrt{3}$��
��ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ�����C��������AB���ӳ��߽��ڵ�P������AC������A=30�㣬PC=3����BP�ij�Ϊ$\sqrt{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com