
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行于⊙O的弦MB,连接DM并延长交x轴于点C.
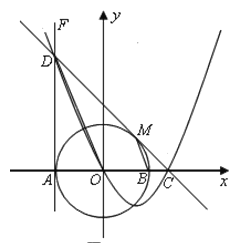
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求经过D、O、C三点的抛物线的解析式.
(3)若坐标平面内的点P,使得以点P和三点D、O、C为顶点的四边形是平行四边形,求P点的坐标.
【答案】(1)见解析;(2)y=![]() x2-
x2-![]() x;(3)P1(-
x;(3)P1(-![]() ,4),P2(
,4),P2(![]() ,4),P3(
,4),P3(![]() ,-4)
,-4)
【解析】
(1)连接OM,根据DO∥MB即可证得△AOD≌△MOD,从而得出∠OMD=∠OAD,因为DA⊥OA,即可得OM⊥CD;
(2) 设MC=x,可证得△OMC∽△DAC,利用相似三角形的性质得出OC=2x-2,利用勾股定理即可列出方程即可求解;
(3)要使以点P和三点D、O、C为顶点的四边形是平行四边形,则分三种情况讨论:①当DP∥OC,DC为对角线时,②当PD∥OC,DO为对角线时,③当DC∥OP,OC为对角线时,根据每种情况求解即可.
(1) 直线DC与⊙O相切.证明如下:
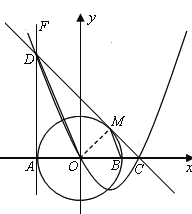
如图,连接OM,则OM=OB,
∴∠OMB=∠OBM.
∵DO∥MB,
∴∠AOD=∠OBM, ∠MOD=∠OMB,
∴∠AOD=∠MOD.
又∵OA=OM,OD=OD,
∴△AOD≌△MOD,
∴∠OMD=∠OAD.
而DA⊥OA,
∴∠OAD=90°,
∴∠OMD=90°,即OM⊥CD,
∴直线DC与⊙O相切.
(2)设MC=x.
∵∠OMC=∠DAC=90°,∠OCM=∠DCA,
∴△OMC∽△DAC,
∴![]() =
=![]() .
.
∵OM=OA=2,DA=4,AC=OA+OC=2+OC,
∴![]() =
=![]() ,
,
∴OC=2x-2.
在Rt△OMC中,
∵OM2+MC2=OC2,
∴22+x2=(2x-2)2,
解得x1=![]() ,x2=0(舍去),
,x2=0(舍去),
∴OC=2×![]() -2=
-2=![]() ,
,
∴C(![]() ,0).
,0).
因为抛物线经过坐标原点O,所以c=0,可设抛物线的解析式为y=ax2+bx,将(-2,![]() ,0)代入,得
,0)代入,得
 解之,得
解之,得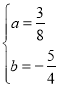 .
.
∴y=![]() x2-
x2-![]() x.
x.
(3)①当DP∥OC,DC为对角线时
∵D (-2,4),C(![]() ,0),
,0),
∴AO=OB=2,OC=![]()
∴P1(![]() ,4)
,4)
②当PD∥OC,DO为对角线时
∵DP2=OC=![]()
∴P2(-![]() ,4)
,4)
③当DC∥OP,OC为对角线时
同理可得P3(![]() ,-4).
,-4).
故P点坐标为:P1(![]() ,4),P2(-
,4),P2(-![]() ,4),P3(
,4),P3(![]() ,-4)
,-4)


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠A=90°,AB=12cm,AC=6cm,点P沿AB边从点A开始向点B以每秒2cm的速度移动,点Q沿CA边从点C开始向点A以每秒1cm的速度移动,P、Q同时出发,用t表示移动的时间.
中,∠A=90°,AB=12cm,AC=6cm,点P沿AB边从点A开始向点B以每秒2cm的速度移动,点Q沿CA边从点C开始向点A以每秒1cm的速度移动,P、Q同时出发,用t表示移动的时间.
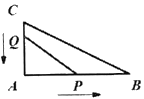
(1)当t为何值时,△QAP为等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
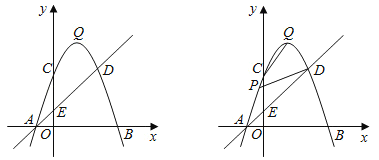
(1)求该抛物线的解析式及顶点![]() 的坐标.
的坐标.
(2)连接![]() ,直接写出线段
,直接写出线段![]() 与线段
与线段![]() 的数量关系和位置关系.
的数量关系和位置关系.
(3)连接![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(4)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出点
为等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
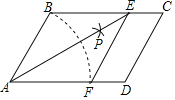
【题目】如图,在平行四边形ABCD中,以A为圆心,AB长为半径画弧交AD于点F;再分别以B、F为圆心,大于![]() 的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF是菱形.
的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF是菱形.
(1)求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为8,![]() ,求∠C的大小.
,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这两中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
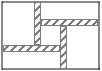
【题目】工人师傅童威准备在一块长为60,宽为48的长方形花圃内修建四条宽度相等,且与各边垂直的小路.四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的8倍.若四条小路所占面积为160.设小路的宽度为x,依题意列方程,化为一般形式为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数![]() 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )
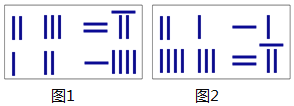
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com