
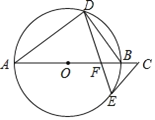
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径长为5,BF=2,求EF的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OE,易得∠ADB=90°,证明∠BOE=∠A,联立∠C=∠ABD可求证.
(2)连接BE,根据同弧所对的圆周角先证明△BEF∽△BOE,根据相似三角形的性质求出EF的长度.
解:(1)连接OE,
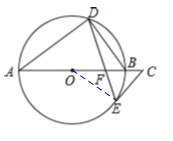
∵AB是![]() 的直径,
的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
由图可知∠BOE=2∠BDE
又∵∠A=2∠BDE
∴∠A=∠BOE
∵∠C=∠ABD
∴∠BOE+∠C=90°
∴OE⊥EC
∴CE是⊙O的切线.
(2)连接BE,
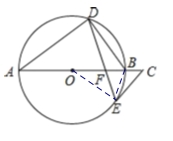
有图可知∠BED=∠A=∠BOE,
∴△BEF∽△BOE
∴![]()
∵OB=OE=5,BF=2
∴BE=EF
∴EF2=OE·BF=10
∴EF=![]()
故答案为:(1)证明见解析;(2)![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
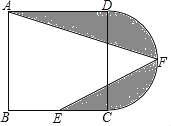
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y (米)与时间t (分钟)之间的函数关系如图所示,根据图象信息知,点A的坐标是__________;
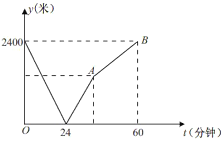
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )
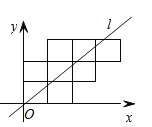
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP',连接CP',则线段CP'的最小值为( )
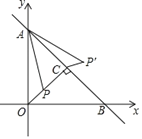
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以BC为直径作⊙ O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若BG=OB,AC=6,求BF的长.
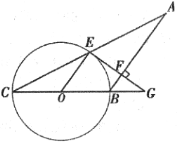
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠C=30°,⊙O的半径为6,求弓形AF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com