
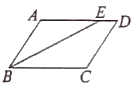
【题目】如图已知BE平分∠ABC,E点在线段AD上,∠ABE=∠AEB,AD与BC平行吗?为什么?
解:因为BE平分∠ABC(已知)
所以∠ABE=∠EBC ( )
因为∠ABE=∠AEB( )
所以∠ =∠ ( )
所以AD∥BC ( )
 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点分别是A(2,0)、B(0,4)、C(-3,0),把△ABC沿x轴向右平移4个单位,得到△A1B1C1.
(1)在图中以黑点为原点建立平面直角坐标系,画出△ABC和△A1B1C1;
(2)写出A1、B1、C1各点的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,将
,将![]() 如图摆放,使得
如图摆放,使得![]() 的两条边分别经过点
的两条边分别经过点![]() 和点
和点![]() .
.

(1)当将![]() 如图1摆放时,则
如图1摆放时,则![]() _________度.
_________度.
(2)当将![]() 如图2摆放时,请求出
如图2摆放时,请求出![]() 的度数,并说明理由.
的度数,并说明理由.
(3)能否将![]() 摆放到某个位置时,使得
摆放到某个位置时,使得![]() 、
、![]() 同时平分
同时平分![]() 和
和![]() ?直接写出结论_______(填“能”或“不能”)
?直接写出结论_______(填“能”或“不能”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
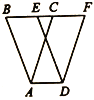
【题目】如图,在△ABC中,![]() ,将△ABC以每秒2cm的速度沿
,将△ABC以每秒2cm的速度沿![]() 所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使
所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使![]() 成立,则
成立,则![]() 的值为_____秒.
的值为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形。
,所以这个三角形是常态三角形。
(1)若△ABC三边长分别是2,![]() 和4,则此三角形_________常态三角形(填“是”或“不是”);
和4,则此三角形_________常态三角形(填“是”或“不是”);
(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为__________________(请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD,EH在直线l上,且AD=5cm,EH=4cm,EF=3cm.保持正方形ABCD不动,将矩形EFGH沿直线l左右移动,连接BF,CG,则BF+CG的最小值为_____________cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商店计划从厂家购进![]() 两种不同型号的电风扇,若购进8台
两种不同型号的电风扇,若购进8台![]() 型和20台
型和20台![]() 型电风扇,需资金7600元,若购进4台
型电风扇,需资金7600元,若购进4台![]() 型和15台
型和15台![]() 型电风扇,需资金5300元.
型电风扇,需资金5300元.
(1)求![]() 型电风扇每台的进价各是多少元;
型电风扇每台的进价各是多少元;
(2)该商店经理计划进这两种电风扇共50台,而可用于购买这两种电风扇的资金不超过12800元,根据市场调研,销售一台![]() 型电风扇可获利80元,销售一台
型电风扇可获利80元,销售一台![]() 型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com