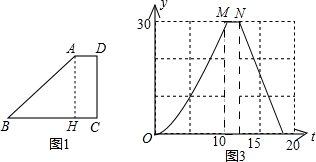
解:(1)设动点出发t秒后,点P到达点A且点Q正好到达点C时,BC=BA=t,
则S
△BPQ=

×t×6=30,
所以t=10(秒).
则BA=10(cm),
过点A作AH⊥BC于H,
则四边形AHCD是矩形,
∴AD=CH,CD=AH=6cm,
在Rt△ABH中,BH=8cm,
∴CH=2cm,
∴AD=2cm;
(2)可得坐标为M(10,30),N(12,30);
(3)当点P在BA边上时,
y=

×t×tsinB=

t
2×
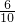
=
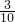
t
2(0≤t<10);
当点P在DC边上时,
y=

×10×(18-t)=-5t+90(12<t≤18);
图象见下.
分析:(1)P在AD边上运动时,三角形BQP以BQ为底边,以CD的长为高,因此可根据三角形BQP的面积为30cm
2求出BC=10cm,而P、Q速度相同,P到A的时间与Q到C的时间相同,因此BA=BC.那么BA=BC=10cm.
求AD的长可通过构建直角三角形来求解.过A作AH⊥BC与H,那么在直角三角形ABH中,AH=CD=6cm,BA=10cm;因此可根据勾股定理求出BH=8cm,那么AD=BC-BH=2cm.
(2)根据(1)得出的BA、AD的长,可求出P从B运动到A,从A运动到D分别用了多少时间,即可求出M、N的横坐标,已知M、N的纵坐标为30,由此可得出M、N的坐标.
(3)三角形BQP中,BQ=t,BP=t,以BQ为底边的高,可用BP•sinB来表示,然后可根据三角形的面积计算公式得出关于y,t的函数关系式.
点评:本题结合梯形、三角形的相关知识考查了二次函数的综合应用.借助函数图象表达题目中的信息,读懂图象是关键.

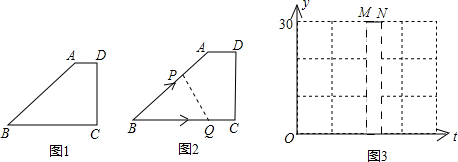
 解:(1)设动点出发t秒后,点P到达点A且点Q正好到达点C时,BC=BA=t,
解:(1)设动点出发t秒后,点P到达点A且点Q正好到达点C时,BC=BA=t, ×t×6=30,
×t×6=30, ×t×tsinB=
×t×tsinB= t2×
t2× =
= t2(0≤t<10);
t2(0≤t<10); ×10×(18-t)=-5t+90(12<t≤18);
×10×(18-t)=-5t+90(12<t≤18);

 春雨教育同步作文系列答案
春雨教育同步作文系列答案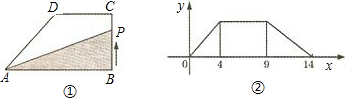
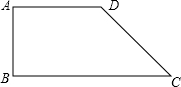 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为