
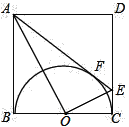
【题目】如图,在正方形ABCD中,以BC为直径的正方形内,作半圆O,AE切半圆于点F交CD于E
(1) 求证:AO⊥EO
(2) 连接DF,求tan∠FDE的值
【答案】(1)证明见解析;
(2)tan∠FDE的值是![]()
【解析】试题分析:(1)、根据切线的性质得出∠BAO=∠FAO,∠CEO=∠FEO,根据四边形的性质得出∠BAE+∠CEA=180°,从而说明∠DAF+∠OEF=90°,得出垂直;(2)、设OB=OC=2,则AB=4,根据△AOB和△OEC全等得出CE=EF=1,DE=3,AE=5,过点F作FG⊥DE于G,则FG∥AD,根据平行线截线段成比例得出FG、EG和DG的长度,最后根据三角函数的计算法则得出答案.
试题解析:(1) ∵∠ABC=∠DCB=90° ∴AD、CD均为半圆的切线
连接OF ∵AE切半圆于E ∴∠BAO=∠FAO,∠CEO=∠FEO ∵∠BAE+∠CEA=180°
∴∠DAF+∠OEF=90° ∴∠AOE=90° ∴AO⊥EO
(2) 设OB=OC=2,则AB=4 ∵Rt△AOB∽Rt△OEC ∴CE=EF=1,DE=3,AE=5
过点F作FG⊥DE于G ∴FG∥AD
∴![]() 即
即![]() ∴FG=
∴FG=![]() ,EG=
,EG=![]() ,DG=
,DG=![]() ∴tan∠FDE=
∴tan∠FDE=![]()


科目:初中数学 来源: 题型:
【题目】将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( )
A.y=3(x﹣2)2﹣1
B.y=3(x﹣2)2+1
C.y=3(x+2)2﹣1
D.y=3(x+2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于( )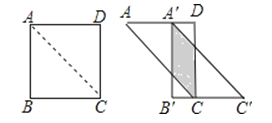
A.4
B.6或4
C.8
D.4或8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运动属于平移的是( )
A. 空中放飞的风筝
B. 飞机的机身在跑道上滑行至停止
C. 运动员投出的篮球
D. 乒乓球比赛中高抛发球后,乒乓球的运动方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC各顶点的坐标分别为A(﹣2,5)B(﹣5,﹣2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′. 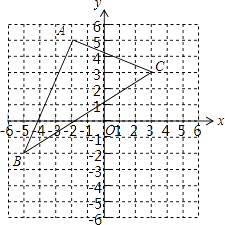
(1)在图中画出第二次平移之后的图形△A′B′C′;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.

(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°. 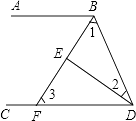
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com