
【题目】在一个三角形中,各边和它所对角的正弦的比相等.即![]() .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:
在![]() 中,若∠A=45°,∠B=30°,a=6,求b.
中,若∠A=45°,∠B=30°,a=6,求b.
【答案】(1)![]() 是等边三角形,证明见解析;
是等边三角形,证明见解析;
(2)![]()
试题分析:(1)先根据路程=速度×时间求出A1A2=30![]() ×
×![]() =10
=10![]() ,又A2B2=10
,又A2B2=10![]() ,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°-15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10
,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°-15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10![]() ,那么∠B1A1B2=105°-60°=45°.然后在△B1A1B2中,根据阅读材料可知,
,那么∠B1A1B2=105°-60°=45°.然后在△B1A1B2中,根据阅读材料可知, ![]() ,求出B1B2的距离,再由时间求出乙船航行的速度.
,求出B1B2的距离,再由时间求出乙船航行的速度.
试题解析:(1) ![]() 是等边三角形,理由如下:
是等边三角形,理由如下:
连结A1B2.
∵甲船以每小时30![]() 海里的速度向正北方向航行,航行20分钟到达A2,
海里的速度向正北方向航行,航行20分钟到达A2,
∴A1A2=30![]() ×
×![]() =10
=10![]() ,
,
又∵A2B2=10![]() ,∠A1A2B2=60°,
,∠A1A2B2=60°,
∴△A1A2B2是等边三角形;
(2)过点B作B1N∥A1A2,如图,
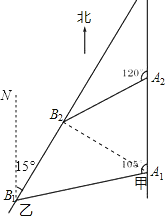
∵B1N∥A1A2,
∴∠A1B1N=180°∠B1A1A2=180°105°=75°,
∴∠A1B1B2=75°15°=60°.
∵△A1A2B2是等边三角形,
∴∠A2A1B2=60°,A1B2=A1A2=10![]() ,
,
∴∠B1A1B2=105°60°=45°.
在△B1A1B2中,
∵A1B2=10![]() ,∠B1A1B2=45°,∠A1B1B2=60°,
,∠B1A1B2=45°,∠A1B1B2=60°,
由阅读材料可知, ![]() ,
,
解得B1B2=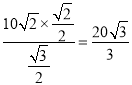 ,
,
所以乙船每小时航行: ![]() ÷
÷![]() =
= ![]() 海里。
海里。


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②SABCD=AC·BC;③OE∶AC=![]() ∶6;④S△OCF=2S△OEF.成立的个数有( )
∶6;④S△OCF=2S△OEF.成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )

A.20海里 B.40海里 C.![]() 海里 D.
海里 D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是CD的延长线上一点,连接BE交AD于点F,且AF=2FD.
(1)求证:△ABF∽△CEB;
(2)若△CEB的面积为9,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
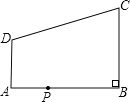
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com